목록물리학 (132)
설군의연구소
 원통이 혼자 구를 때의 마찰력의 방향
원통이 혼자 구를 때의 마찰력의 방향
안녕하세요, 설군입니다. 이전 글에서, 원통을 잡아딩기며 굴릴 때의 마찰력의 방향에 대해서 이야기 한 적이 있습니다. (https://seolgoons.tistory.com/70) 이 경우와는 다르게, 빗면에서 원통이 중력만을 받으며 굴러가는 상황에 대해서 생각해봅시다. 이 상황에서는 마찰력의 방향이 달라요. 이와 같이 질량이 \(M\), 반지름이 \(R\)인 원통이 빗면에서 *미끄러지지 않고 구르는* 경우를 생각해보면, 다음과 같이 물체에 작용하는 힘 그림을 그려볼 수 있습니다. 빗면 위의 물체가 받는 힘은, 중력의 빗면 방향 성분(\(x\) 방향 성분)과, 그것에 수직인 방향의 수직항력 \(N\)을 받고, 그리고 그것과 상쇄되는 중력의 성분 \(Mg \cos(\theta\)\)를 받을 거예요. 물론 ..
 실패 문제에서 마찰력의 방향
실패 문제에서 마찰력의 방향
안녕하세요, 설군입니다. 실패 문제라는 건 다음과 같은 상황을 말합니다. 평면에서 실이 감긴 원통을 잡아당기는 상황입니다. 이 상황에는 실이 풀리면서 회전하며 평지를 굴러갈거예요. 이걸 옆에서 본 모습은 다음과 같이 그릴 수 있습니다. 물체가 미끄러지지 않는 구름 조건을 만족하며 운동하고 있다고 합시다. 그 말은 다음 두 식이 성립한다는 의미입니다. $$ v=R\omega, \quad a = R\alpha $$ 마찰력이 작용하지 않는 상황이라고 생각해볼까요? 그렇다면 직선 운동 방정식과 회전 운동 방정식을 각각 세울 때 다음과 같이 세울 수 있습니다. 먼저 직선 운동 방정식을 세우기 위해서 알짜힘을 생각해보면, 물체가 운동하는 방향으로 힘 \(F\)만 받고 있으므로 식은 $$ F=Ma $$ 로 세워집니다..
 두께가 있는 고리의 관성 모멘트에 대한 해석
두께가 있는 고리의 관성 모멘트에 대한 해석
안녕하세요, 설군입니다. 두께가 있는 고리의 관성 모멘트는 다음과 같습니다. $$ I = \frac{1}{2} M(R_1^2 +R_2^2) $$ 얼핏 생각하기에, 내경과 외경의 차이로 계산해야 되므로, 괄호의 항은 \(R_2^2 - R_1^2\)일 것 같지만, 계산해보면 합이 맞습니다. 이렇게 생각해보면 됩니다. 두께가 있는 고리의 내경과 외경을 생각해보면, 내경은 외경보다 클 수 없습니다. 즉 \(R_1 < R_2\)입니다. 그렇다면 만약 \(R_1 = R_2\)라면 두께가 없는 고리와 같아지는 셈이고, \(R_1 = 0\)이라면 속이 꽉찬 원통과 같아지는 셈입니다. * \(R_1 = R_2\)라면, 두께가 없는 고리와 같아진다. $$ I = \frac{1}{2} M(R_1^2+R_2^2) = \fra..
 정지 마찰력과 운동 마찰력
정지 마찰력과 운동 마찰력
안녕하세요, 설군입니다. 마찰력 문제를 풀 때에는 물체가 정지한 상황에서 받는 마찰력인지, 운동하고 있는 상황에서 받는 마찰력인지를 꼭 구별해야 합니다. 운동하고 있는 상황에서 받는 마찰력은 가속운동이나 등속운동 모두 적용됩니다. * 정지 마찰력 먼저 정지한 상황에서 받는 마찰력을 생각해봅시다. 물체가 정지한 상황에서 받는 마찰력이라는 말은, 물체가 외부 힘을 받고있는데 그것에 버티기 위해서 반대 방향으로 마찰력이 작용하는 상황입니다. 예를 들어 빗면에 가만히 놓인 물체같은 경우가 있습니다. 그림과 같이 질량이 \(M\)인 물체가, 경사각이 \(\theta\)인 빗면에 놓여 있는 상황입니다. 이 때 물체가 마찰력을 받으며 정지해 있는 상황을 생각해봅시다. 빗면에 놓인 물체는 중력을 받고, 마찰력도 받으며..
 경사면에서 구르는 물체의 운동
경사면에서 구르는 물체의 운동
안녕하세요, 설군입니다. 경사면에서 물체가 구름운동 할 때의 상황을 분석해봅시다. 위의 그림과 같이 어떤 경사면에 원통이 놓여있는 상황을 생각해봅시다. 원통의 총 질량과 반지름은 \(M\), \(R\)이고, 원통의 높이는 우리가 오늘 다룰 회전 운동 문제에서는 중요하지 않습니다. 높이가 \(h\)인 경사면의 꼭대기에서 원통을 가만히 놓았다면 원통이 굴러갈 거예요. 이 때 이상적인 상황을 가정하기 위해서, 원통이 경사면에서 미끄러지지 않고 회전운동을 하며 굴러간다고 생각해봅시다. 역학적 에너지 보존 법칙을 이용해서, 이 원통이 경사면의 끝에 도달했을 때의 속력을 구해봅시다. $$ Mgh = \frac{1}{2} Mv^2 + \frac{1}{2} I \omega^2 $$ 와 같이, 원통이 처음에 가지고 있던..
 관성 모멘트의 개념
관성 모멘트의 개념
안녕하세요, 설군입니다. 관성 모멘트라는 물리량은 직선 운동에서 질량에 대응됩니다. 질량이 큰 물체는 관성이 커서, 가속시키는 데에 큰 힘이 들고 질량이 작은 물체는 관성이 작아서, 가속시키는 데에 작은 힘이 듭니다. 관성 모멘트가 큰 물체는 회전 관성이 커서, 회전 운동 시키는 데에 큰 토크가 들고 관성 모멘트가 작은 물체는 회전 관성이 작아서, 회전 운동 시키는 데에 작은 토크가 듭니다. 관성 모멘트를 이야기할 때에는 물체가 크기를 가지고, 회전을 하는 상황이기 때문에 회전축이 어디인지 꼭 말해주어야 합니다. 회전축이 어디냐에 따라 물체를 회전시키는 게 더 어려울 수도 있고 쉬울 수도 있어요. 간단한 다음 예시를 생각해봅시다. 이렇게 생긴 아령이 있고, 중앙 부분을 한 손으로 잡고 손목으로 빙빙 회전..
 속도-시간 그래프에서의 넓이
속도-시간 그래프에서의 넓이
안녕하세요, 설군입니다.속도-시간 그래프에서의 넓이, 기울기 등을 잘 구하고 쓸 줄 아는것이 중요합니다.예를 들어 위와 같이 물체의 속도-시간 그래프가 주어졌을 때, 물체가 0-6 초 동안 이동한 변위를 구하라고 한다면?변위의 개념과, 이동거리의 개념을 일단 잘 알아야 합니다. 변위는 말 그대로 위치의 변화값을 의미합니다.물체가 예를들어 $x$ 축 상에서만 운동을 하고 있을 때,물체의 처음 위치가 $x=1$ 이었고, 운동 과정이 어쨌건간에 최종 위치가 $x=5$ 가 되었다면변위는$$ \Delta x = x_f - x_i = 5 - 1 = 4 $$입니다. 변위는 4 인 것이죠. 이동거리는, 운동 과정 중에 이동한 전체 거리를 의미합니다. 이번에는 운동 과정이 중요한 것이죠. 앞으로..
 전반사, 굴절률과 임계각
전반사, 굴절률과 임계각
안녕하세요, 설군입니다. 전반사라는 건, 빛이 밀한매질을 지나 소한매질을 통과하는 과정에서, 굴절되지 않고 반사되어버리는 현상입니다. 일반적으로 빛이 밀한 매질에서 소한 매질로 통과하는 경우는 다음과 같습니다. 예를 들어, 물에서 공기로 통과하는 경우 이런 상황입니다. 그런데 항상 입사각이 더 작은지, 굴절각이 더 작은지를 생각하게 되고 그림을 어떻게 그려야 할지 고민하게 됩니다. 물에서의 입사각이 더 작고 공기에서의 굴절각이 더 컸던가? 아니면 물에서의 입사각이 더 크고 공기에서의 굴절각이 더 작았던가? 하면서 말이죠. 밀한 매질에서의 각도가 더 큽니다. 스넬의 법칙을 떠올리면 다음과 같이 쓸 수 있습니다. 전반사에 대해서 이야기하려고 하는데요, 신기하게도 밀한 매질에서 소한 매질로 빛이 지나갈 때, ..
 운동 방정식을 각각의 물체에 대해 적용하기
운동 방정식을 각각의 물체에 대해 적용하기
안녕하세요, 설군입니다. 뉴턴의 제 2법칙인 가속도의 법칙입니다. 가속도의 법칙은 어떤 물체가 받는 알짜힘과 그 물체의 질량, 그리고 그 물체의 현재 가속도 사이의 관계를 나타내주는 식입니다. 어떤 문제를 풀어야 하는 상황에 놓였을 때, 내가 분석하고자 하는 물리계에 여러 물체가 다양한 힘을 받고있을 수 있습니다. 이 때, 제일 간단하게 그 물체의 운동을 분석하는 방법은, 수많은 물체 중 내가 분석하고자 하는 물체 하나를 고른 다음 F = ma 를 적용하는 것입니다. 물리학 문제를 풀 때 이 식을 단순히 F = ma 라고 암기하지 말고, 그 말뜻을 풀어서 이해해야 합니다. 어떤 물체가 받는 알짜힘은 그 물체의 질량 곱하기 그 물체의 가속도이다. 이렇게 이해해야 하는데, 그 물체가 받는 여러 힘 중에 다른..
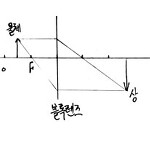 물리 2 - 렌즈에서의 상
물리 2 - 렌즈에서의 상
안녕하세요, 설군입니다. 개인적으로는 렌즈가 더 어렵다고 생각됩니다. 거울은 빛을 반사하여 상이 생기게 하는거였다면 렌즈는 빛이 굴절(렌즈를 통과)되면서 상이 생기는것이죠 볼록렌즈는 빛을 모이게 하고 오목렌즈는 빛을 퍼지게 합니다. 사실 실제 렌즈는 두께가 있어서 우리가 책으로 배우는 렌즈의 굴절과는 약간 다른데 책에서 배우는 렌즈는 두께가 아주아주아주 얇다고 가정하여 '한 번'굴절한다고 놓고 풀어가고있는 것입니다. (그래서 저도 거울이나 렌즈를 그릴때 그냥 일자로 그립니다. 어정쩡하게 그렸다가 광선 꺾어그리기가 힘들어서요...) 1. 광축에 나란하게 입사한 광선은 렌즈를 지나고 나서 초점을 지나거나/ 초점에서 나온것처럼 진행한다. 2. 초점을 지나거나 초점을 향해 입사한 광선은 렌즈를 지나고나서 광축에..
