설군의연구소
직선 전하가 만드는 전기 퍼텐셜 본문
안녕하세요, 설군입니다.

이번에는 유한한 길이의 직선에 전하가 콕콕콕 박혀 있는, 직선 전하 분포가 만드는 전기 퍼텐셜을 구해봅시다.
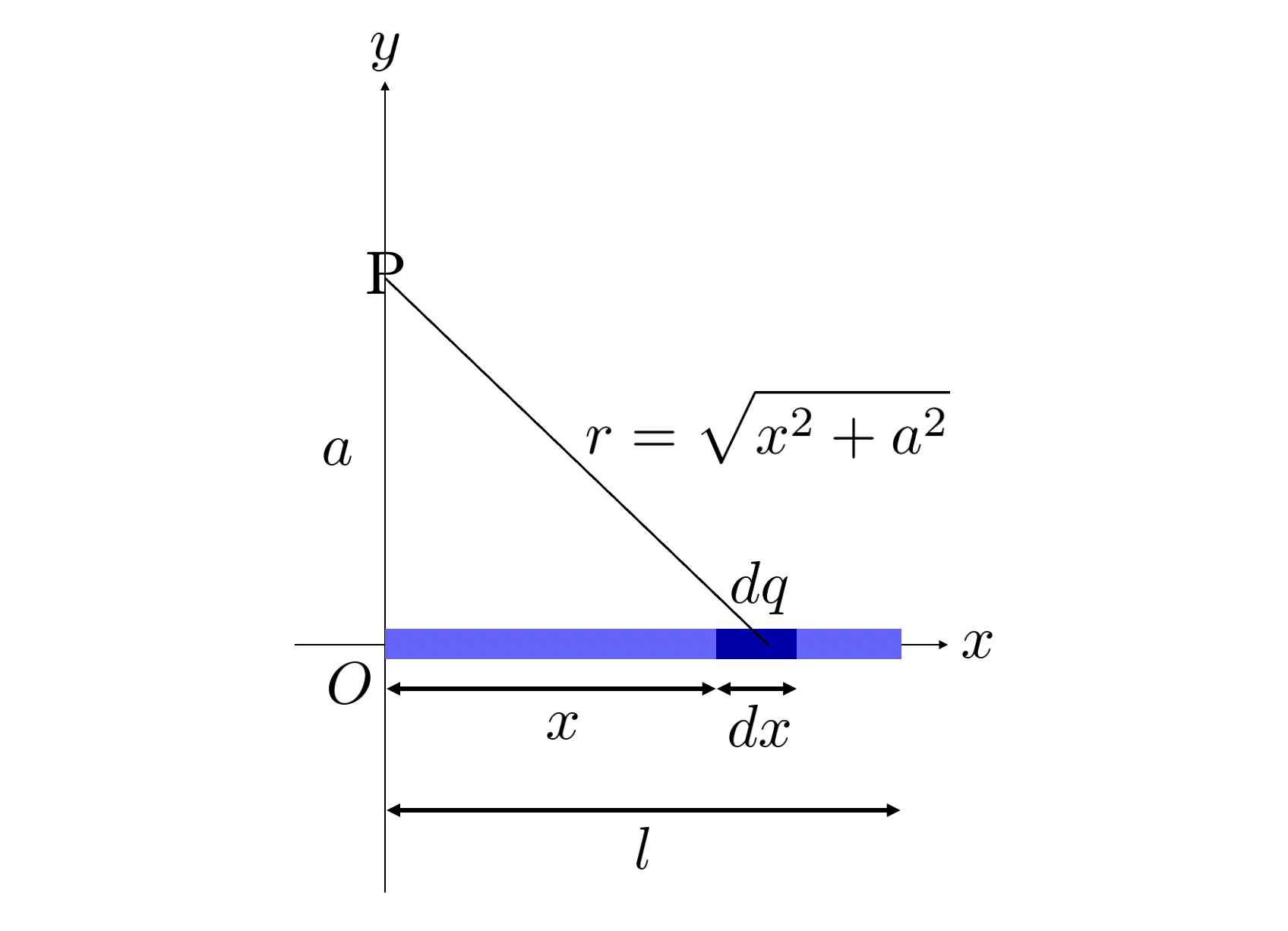
총 전하량이 $Q$이고, 총 길이가 $l$인 직선 전하가 있습니다. 이 직선 전하의 전하 분포가 균일하다고 하면, 이 직선의 전하 밀도가 균일하다는 이야기입니다. 선 전하 밀도는 다음과 같이 정의합니다.
$$ \text{(선 전하 밀도)}= \frac{\text{(총 전하량)}}{\text{(총 길이)}} $$
$$ \lambda = \frac{Q}{l} $$
이번에도 역시 작은 전하 조각이 만드는 전기 퍼텐셜을 써 보면 다음과 같이 쓸 수 있습니다.
$$ dV = k \frac{dq}{r} = k \frac{dq}{\sqrt{a^2+x^2}} $$
여기서 전하 조각의 전하량 $dq = \lambda dx$로 쓸 수 있습니다. 왜냐하면 $ \text{(전하량)} = \text{(선 전하 밀도)} \times \text{(길이)} $가 되기 때문입니다.
따라서 총 직선 전체가 만드는 전기 퍼텐셜은
$$ V = \int_0^l k \frac{\lambda dx}{\sqrt{a^2+x^2}} $$
으로 쓸 수 있습니다. 이 적분을 수행하기 위해서 다음과 같이 치환합니다.

직각 삼각형을 하나 생각해서,
$$ \tan (\theta) = \frac{x}{a} $$
로 둔 후에,
$$ a \tan (\theta) = x $$
이므로,
$$ a \sec ^2 (\theta) d\theta = dx $$
로 생각합니다. 그리고 $\sqrt{a^2+x^2} = a \sec (\theta) $가 되겠죠? 그렇다면 적분식은,
$$ \begin{split} V =& \int_0^l k \frac{\lambda dx}{\sqrt{a^2+x^2}} \\ =& k \lambda \int \frac{a \sec^2 (\theta) d \theta}{a \sec (\theta)} \\ =& k \lambda \int \sec (\theta) d \theta \end{split} $$
이 되는데, $\sec (\theta)$를 적분하기 위해서, 위의 적분 식의 분모 분자에 $\sec (\theta) + \tan(\theta)$를 곱해줍니다.
$$ k \lambda \int \frac{\sec ^2 (\theta) + \tan (\theta)}{\sec (\theta) + \tan(\theta)} d\theta $$
여기서 분자 부분은 신기하게도
$$ \frac{d}{d \theta} ( \sec (\theta) + \tan (\theta)) = \sec (\theta) \tan (\theta) + \sec^2 (\theta) $$
이므로, 저 적분은 $\int \frac{x'}{x} dx$꼴입니다. 즉 로그가 결과입니다. 따라서
$$ V = k \lambda \int \frac{(\sec (\theta) + \tan (\theta))'}{\sec(\theta) + \tan(\theta)} d\theta = k \lambda \ln \left[ \sec(\theta) + \tan(\theta) \right] $$
가 되고, 치환한 것을 다시 되돌려 주면
$$ V = k \lambda \left[ \ln \left( \frac{\sqrt{a^2+x^2}}{a} + \frac{x}{a} \right) \right]_{x=0}^{x=l} = k \lambda \left[ \ln \left( \sqrt{a^2+x^2} + x\right) - \ln (a) \right]_{x=0}^{x=l} $$
이고,
$$ = k \lambda \left[ \ln \left( \frac{l + \sqrt{a^2+l^2}}{a} \right) \right] $$
가 됩니다. 만약 전기장을 구하고자 한다면, 우리가 지금 문제를 푼 상황이 바로 $y$축 위의 임의의 거리 $a$에서의 전기장을 구하는 상황이었으므로, 여기서 $a$를 $y$로 대체하면 $y$에 대한 미분을 수행할 수 있게 됩니다. 그렇게 하면 막대가 만드는 전기장의 $y$성분을 구할 수는 있는데, 우리가 방금 푼 문제의 지점 P에서는 전기장이 $x$성분도 존재할텐데...
우리의 결과로는 $x$성분 전기장을 구할 수 없습니다. $x=0$인 위치에 맞춰서 막대를 가져다두었기 때문인데, 이걸 피하기 위해 임의의 위치로 막대를 다시 놓고 문제를 풀어 일반적인 상황에 대한 식을 놓으면 그 때는 구할 수 있습니다.
이건 다음 글에서 한 번 해봅시다!
'물리학 > 일반물리학' 카테고리의 다른 글
| 벡터의 방향을 말하는 방법 (0) | 2022.09.24 |
|---|---|
| 전기적 평형 상태의 도체의 성질 (0) | 2022.09.03 |
| 균일하게 대전된 원판이 만드는 전기 퍼텐셜 (2) | 2022.08.27 |
| 고리 전하 분포가 만드는 전기 퍼텐셜 (0) | 2022.08.27 |
| 전기 쌍극자가 만드는 전기 퍼텐셜 구하기 (0) | 2022.08.06 |





