선 전하 밀도가 각도의 함수인 경우의 전하 분포

반응형

안녕하세요, 설군입니다.

다음과 같이 고리 모양의 전하 분포가 있는데, 그 전하의 선 전하 밀도가 각도에 관한 함수인 경우를 생각해봅시다.

이 때 고리 전하의 총 전하량은 $Q$이고, 원점 $O$에 만드는 전기장을 구하고자 합니다. 가우스 법칙을 이용해서 구할 수는 없고, 쿨롱의 법칙을 이용 해서 적분으로 풀어야 합니다.
먼저, 선 전하 밀도가 각도에 관한 함수라는 건 무슨 말일까요? 각도에 따라 전하 밀도가 다르다는 뜻입니다.
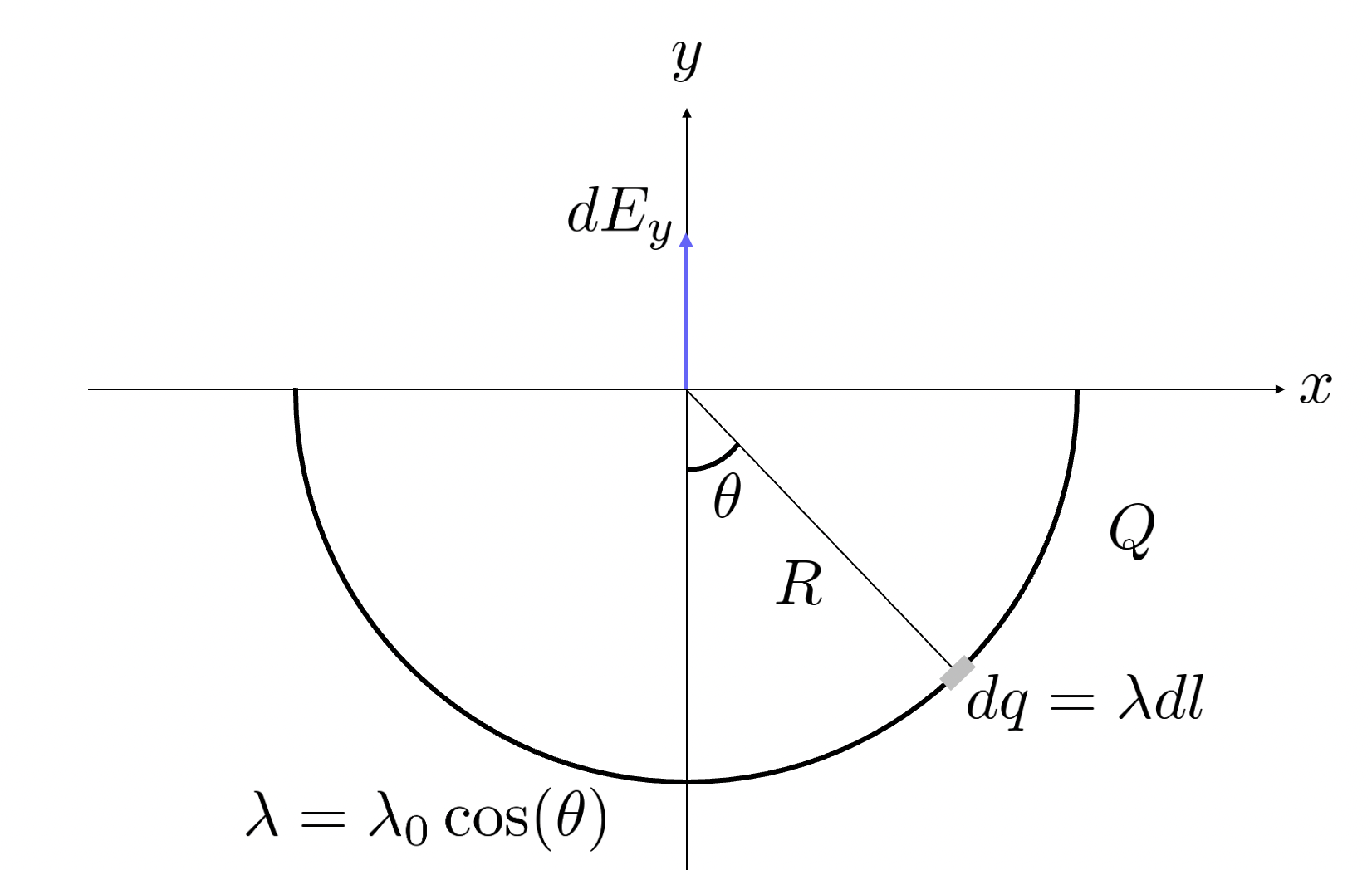
이 때 문제를 풀기 위해서는 각도가 어떻게 정의되냐를 살펴봐야 하는데, 각도는 $+x$축으로부터의 각도라고 생각해봅시다, 그림으로 다시 그려보면 다음과 같은 의미입니다.

각도 $\theta=0^\circ$인 경우에 그 곳의 전하 밀도가 최대이니 색깔을 가장 진하게 표시했고, 각도가 점점 커질 수록 cosine값은 점점 작아져 $\theta=90^\circ$에 도달하는 경우에는 정확하게 $+x$축을 향하는 위치이고, 그 위치에는 전하 밀도가 최소가 되어 0일 거예요. 이게 지금 $xy$좌표 평면에서 4사분면의 얘기고, 3사분면의 경우에도 정확하게 대칭적인 전하 분포를 이루게 됩니다.

문제에 모순이 없는지를 생각해봅시다. 문제에서 고리의 총 전하량이 $Q$라고 했으므로, (잠정적으로)전하는 모두 양전하라고 하고, 그 양전하의 분포가 각도가 증가할수록 점점 감소하는 그런 상황이고, 이 상황에서 원점에서 만드는 전기장을 구하는 것입니다.

쿨롱의 법칙을 적용해서 미소 전하가 만드는 전기장을 구하기 위해 다시 그림을 그려봅시다.

그림으로 표시한 것처럼, 미소 전하 $dq$가 원점에 만드는 전기장은 파란색으로 표시한 화살표와 같은 방향일 테고, 그 크기는 $dE$라고 하겠습니다. 그리고 그 전기장 벡터의 각도는 그림에 표시한 것처럼 전하의 위치 각도와 동일한 각도입니다. 그런데, 이 미소 전하와 정확하게 $y$축에 대칭점인 곳에 있는 미소 전하를 생각해보면,

이렇게 그릴 수 있습니다. 서로 대칭점에 있는 미소 전하가 만드는 전기장 벡터를 살펴보면, 서로 $x$축 성분은 상쇄되고, $y$축 성분만 남습니다. 두 개의 대칭적인 위치에 있는 미소 전하가 만드는 전기장의 $y$축 성분의 크기는 결국, 하나의 미소 전하가 만드는 전기장의 두 배입니다. 그리고 이 사실은 고리 위의 모든 전하에 대해서 적용되므로, 이 고리 전체가 원점에 만드는 전기장의 $x$성분은 아예 없습니다.
그리고 고리의 절반만을 생각해서 그 절반 고리가 원점에 만드는 전기장의 $y$성분만을 구한 후, 그것을 두 배 해주면 문제의 정답이 됩니다. $y$성분은 $\sin (\theta)$ 를 곱해준 것이 됩니다. ($dE_y = dE \sin (\theta)$)
(혹은 고리의 전체를 생각해서 그것이 원점에 만드는 전기장의 $y$성분만을 구한 후, 두 배를 안해줘도 됩니다)

미소 전하가 원점에 만드는 전기장의 전체 성분은

$$d\vec{E} = \frac{1}{4\pi \varepsilon_0} \frac{dq}{R^2}$$

인데, 이것의 $y$성분만을 생각하면

$$dE_y = \frac{1}{4\pi \varepsilon_0} \frac{dq}{R^2} \sin (\theta)$$

그리고 이걸 각도가 $-90^\circ$부터 $90^\circ$까지 적분해주면 됩니다.

$$\begin{split} E_y =& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} dE_y \\ =& \frac{1}{4 \pi \varepsilon_0} \frac{1}{R^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} dq \\=& \frac{1}{4 \pi \varepsilon_0} \frac{1}{R^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \lambda dl \\ =& \frac{1}{4 \pi \varepsilon_0} \frac{\lambda_0}{R^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos (\theta) \sin(\theta) dl \end{split}$$

입니다. 이 때, $dl = R d\theta$이고, $2 \cos(\theta) \sin(\theta) = sin (2 \theta)$이므로,

$$\begin{split} =& \frac{1}{4 \pi \varepsilon_0 } \frac{\lambda_0}{R^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{2} \sin(2\theta) d\theta \\ =& \frac{1}{4 \pi \varepsilon_0 } \frac{\lambda_0}{R^2}\frac{1}{2} \frac{1}{2} \left[ - \cos (2\theta) \right]_{-\frac{\pi}{2}} ^{\frac{\pi}{2}} \\ =& \frac{1}{4 \pi \varepsilon_0 } \frac{\lambda_0}{R^2}\frac{1}{4} \left[ -\cos(\pi) + \cos(-\pi) \right] \\ =& \frac{1}{4\pi\varepsilon_0 } \frac{\lambda_0}{R^2}\frac{1}{2} \end{split}$$

의 결과를 얻을 수 있습니다. 이것이 바로 문제의 고리가 만드는 전기장의 크기입니다!

만약 원점에 전하량 $q$인 양전하 혹은 음전하가 놓여 있고, 고리로부터 양전하에게 가해지는 전기력의 크기와 방향을 묻는다면?

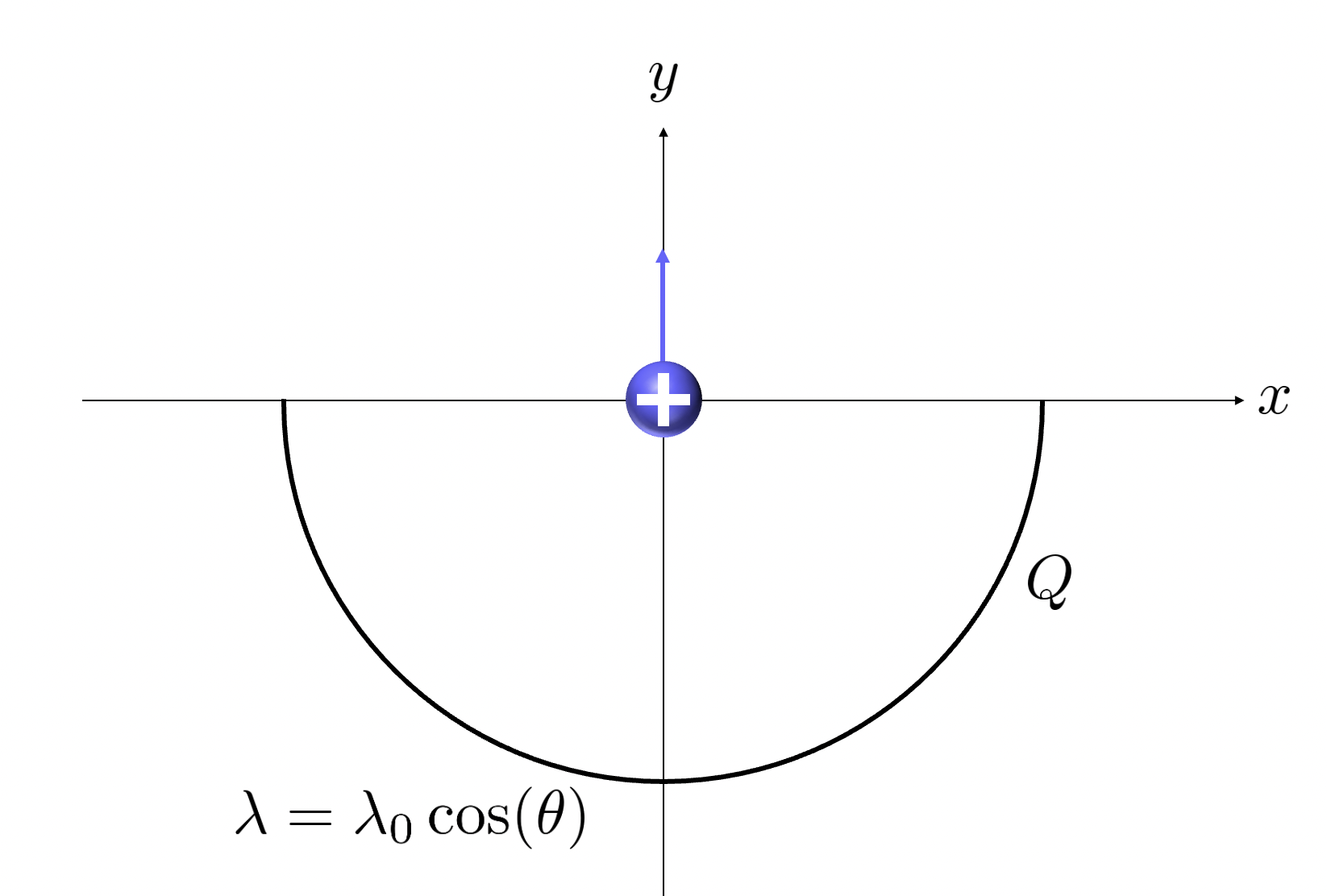
전하량이 $q$인 양전하가 전기장 $E$로부터 받는 전기력의 크기는 $F=qE$이므로, 바로 앞에서 구한 전기장의 크기와 점전하의 전하량을 곱해주면 힘의 크기가 나옵니다. 방향은 우리가 $y$방향밖에 없는 걸 알고 있으므로, 힘의 방향도 그렇습니다.