설군의연구소
가우스 법칙을 사용할 수 없는 경우 본문
안녕하세요, 설군입니다.

대칭적인 전하 분포의 경우에 가우스 법칙을 사용하여 문제를 쉽게 해결할 수 있습니다.
그런데 마치 가우스 법칙을 사용할 수 있을 것 같이 생겼지만 사용할 수 없는 경우가 있습니다.
가우스 법칙을 적용할 때, 내가 풀고자 하는 계의 대칭성을 이용합니다. 그 말은, 내가 풀고자 하는 계의 모양이 적절한 대칭을 가질 때, 그 대칭에 맞게 가우스 곡면을 잡을 수 있다는 것입니다.
가우스 곡면을 잡아서 쉽게 풀 수 있다는 건 결국, 위의 가우스 법칙 식에서 좌변의 적분을 쉽게 계산할 수 있다는 말입니다. 점전하가 만드는 전기장을 구할 때, 구 모양으로 가우스 곡면을 잡는데, 구 모양으로 가우스 곡면을 잡았을 때에는 간단하게 좌변의 전기 플럭스 적분이 으로 구해집니다. 이 이유가 바로 대칭적이기 때문입니다.
점 전하가 만드는 전기장의 모양은 자신을 중심으로 정확하게 구 모양으로 뻗어나가는 모양입니다. 따라서 그 전하를 중심으로 가우스 곡면을 구 모양으로 잡았을 때, 그 전하가 만드는 전기장 화살은 정확하게 구면에 수직하게 통과합니다. 따라서 적분 항의 를 계산할 때, 즉 전기장 벡터와 면적 벡터의 내적을 취할 때, 두 벡터의 방향이 나란하기 때문에 그냥 곱으로 간단해지는 것입니다.
계가 대칭적이지 않다면, 이렇게 모든 전기장이 면적 벡터와 수직인 경우를 만족하는 가우스 곡면을 찾기가 힘듭니다.
따라서 가우스 곡면 자체가 복잡하게 생겼을 테고, 그렇다면 전기 플럭스를 구할 때 각각의 면에 대해 모조리 따로따로 구해서 적분을 취해줘야 합니다.
이것 뿐만 아니라 가우스 법칙을 사용하기 위해서는 다음의 조건 중 몇 가지가 만족하는 경우가 있어야 합니다.
- 내가 잡은 가우스 곡면 위에서의 전기장 값이 상수인 부분이 있어야 한다.
예: 점전하에 대해 구 모양 가우스 곡면을 잡았을 때, 그 가우스 곡면 위에서의 점전하가 만드는 전기장 값은 항상 일정하다.
예: 직선 전하에 대해 원통 모양 가우스 곡면을 잡았을 때, 그 가우스 곡면의 옆면을 통과하는 전기장 값은 항상 일정하다. - 가우스 법칙의 좌변의 적분 항에 있는 내적이 단순한 곱으로 쉽게 표현되는 경우가 있어야 한다.
- 또는 그 적분이 0인 경우가 있어야 한다.
예: 직선 전하에 대해 원통 모양 가우스 곡면을 잡았을 때, 그 가우스 곡면의 윗면(원통 뚜껑)을 통과하는 전기장은 뚜껑의 면적 벡터와 수직이기 때문에 내적이 0이 되어 적분이 0이 된다. - 가우스 곡면상에서 전기장이 0인 경우가 있어야 한다.
몇 가지 예시를 통해 연습을 해보면 어떤 상황에 가우스 법칙을 적용할 수 있는지/없는지를 알 수 있습니다.
* 전기 쌍극자

전기 쌍극자는 위의 그림과 같이 , 의 전하가 임의의 거리 만큼 떨어져 있는 경우를 말합니다. 이 두 전하를 한 묶음으로 전기 쌍극자라고 말합니다. 우리가 하나의 점전하에 대해서 가우스 법칙을 적용할 때에는 그 점전하가 구 모양으로 전기장을 모든 방향으로 뻗어내며 만드는 걸 알고 있으므로, 구 모양으로 가우스 곡면을 잡아 가우스 법칙을 적용할 수 있습니다.
하지만 전기 쌍극자의 경우에는 전기력선을 생각했을 때, 양전하에서 음전하로 꺾이며 들어가는 데다가, 각각의 전하로부터 전기장이 나오거나 들어가는 경우가 있기 때문에 구 모양으로 전기력선이 뻗어나가지 않습니다.
따라서 구 모양으로 가우스 곡면을 잡아 가우스 법칙을 적용할 수 없으며, 어떤 모양을 생각하더라도 가우스 곡면을 잡을 수 없습니다.

한 번 이곳의 중심을 기준으로 구 모양 가우스 곡면을 그려봤습니다. 다시 말하지만 문제를 쉽게 풀기 위해서는 계의 전하들이 만드는 전기장 벡터가 내가 잡은 가우스 곡면에 정확하게 수직으로(면적 벡터와 같은 방향으로) 통과할 때여야 합니다. 그래야 계산이 쉬워지니까 의미가 있으니까요.
그런데 과연 위와 같이 가우스 곡면을 잡았을 때 가우스 곡면을 전기장이 수직으로 통과할까? 를 생각해보면,

이런 부분들을 살펴보았을 때, 수직으로 통과하지 않는다는 것을 알 수 있습니다. 따라서 가우스 법칙을 대칭을 이용해 적용할 수 없습니다.
* 대전된 원판

이번에는 대전된 무한 평판이 아니라, 크기가 무한하지 않은 대전된 원판이 만드는 전기장에 대해 생각해봅시다. 무한 평판이 만드는 전기장을 가우스 법칙을 이용하여 쉽게 구할 때에는 원통형 가우스 곡면을 잡아서 구했었습니다. 그런데 크기가 유한한 대전된 원판의 경우에는 가우스 법칙을 적용할 수 없습니다.
만약 대전된 원판이 엄청나게 크다고 하고, 내가 알고싶은 위치가 원판에 매우 가까운 위치라면, 가우스 곡면을 원판의 크기보다 훨씬 작게 원통형으로 잡으면

이런 식으로 잡아서, 원판에 아주 가까운 곳에서의 전기장을 구할 수는 있습니다. 그런데 이게 바로 무한 평판으로 근사한 경우입니다. 이런 경우 말고, 원판의 끝부분에서의 전기장도 구하고 싶다고 한다면 그곳을 포함하도록 가우스 곡면을 잡아야 합니다. 그런데
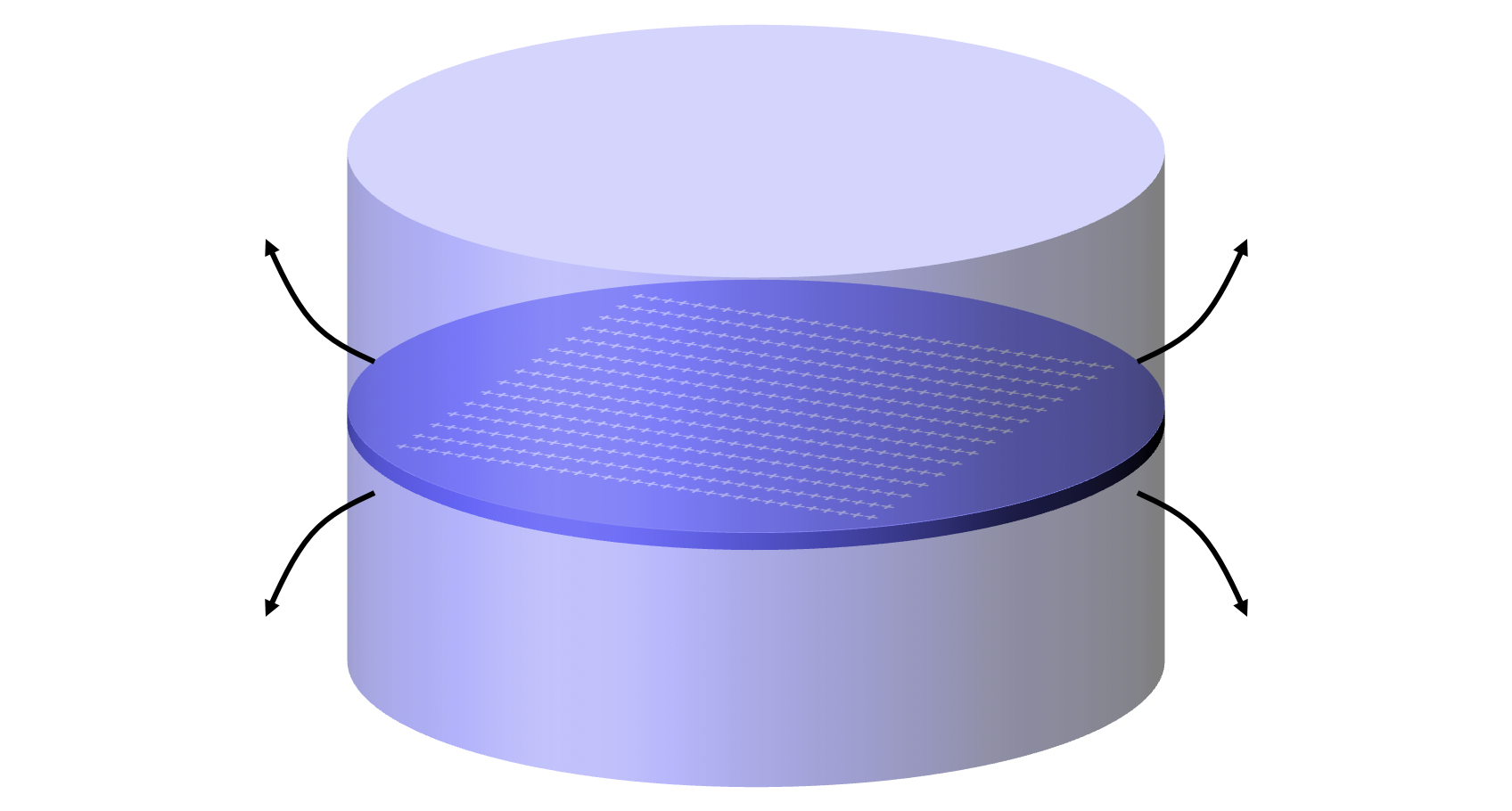
이렇게 원판의 끝부분에서 나오는 전기장 화살이, 내가 잡은 가우스 곡면에 수직하지 않기 때문에 쉽게 구할 수 없습니다.
* 세 개의 점전하
전기 쌍극자도 결국 두 개의 점전하인 것이고, 세 개의 점전하도

위에서 했던 이야기와 같은 이유로 가우스 법칙을 사용하여 이 전하 분포가 만드는 전기장을 쉽게 구할 수 없다는 것을 아실거예요.
'물리학 > 일반물리학' 카테고리의 다른 글
| 구멍 뚫린 구 내부의 전하 (0) | 2022.07.04 |
|---|---|
| 선 전하 밀도가 각도의 함수인 경우의 전하 분포 (0) | 2022.07.02 |
| 면 전하가 만드는 전기장 (A Plane of Charge) (2) | 2022.06.18 |
| 막대 전하가 만드는 전기장 (A cylindrically Symmetric Charge Distribution) (0) | 2022.06.18 |
| 속이 찬 공 모양 전하 (A Spherically Symmetric Charge Distribution) (0) | 2022.06.18 |




