설군의연구소
비오-사바르 법칙을 이용한 고리 도선이 만드는 자기장 구하기 본문
안녕하세요, 설군입니다.

비오-사바르의 법칙은 어떤 전류가 만드는 자기장을 구하는 방법을 알려줍니다.
$$ d\vec{B} = \frac{\mu_0}{4\pi} \frac{I d\vec{l} \times \hat{r}}{r^2} $$
길이가 $dl$로 아주 짧은 막대가, 전류 $I$가 흐르고 그 전류의 방향이 $d\vec{l}$일 때, 그 막대로부터 내가 원하는 지점까지의 방향 벡터가 $\hat{r}$이고 그 거리가 $r$일 때, 그 짧은 막대가 만드는 자기장 $d\vec{B}$를 구하는 공식입니다.
그렇다면 이 짧은 막대들이 모여 도선 하나를 형성한다고 할 때, 그 도선이 만드는 자기장은 짧은 막대들을 모조리 더해주면 됩니다.
따라서 적분식으로 바꾸면
$$ \vec{B} = \frac{\mu_0}{4\pi} \int \frac{I d\vec{l} \times \hat{r}}{r^2} $$
이 됩니다.
다음과 같은 문제를 생각해봅시다.
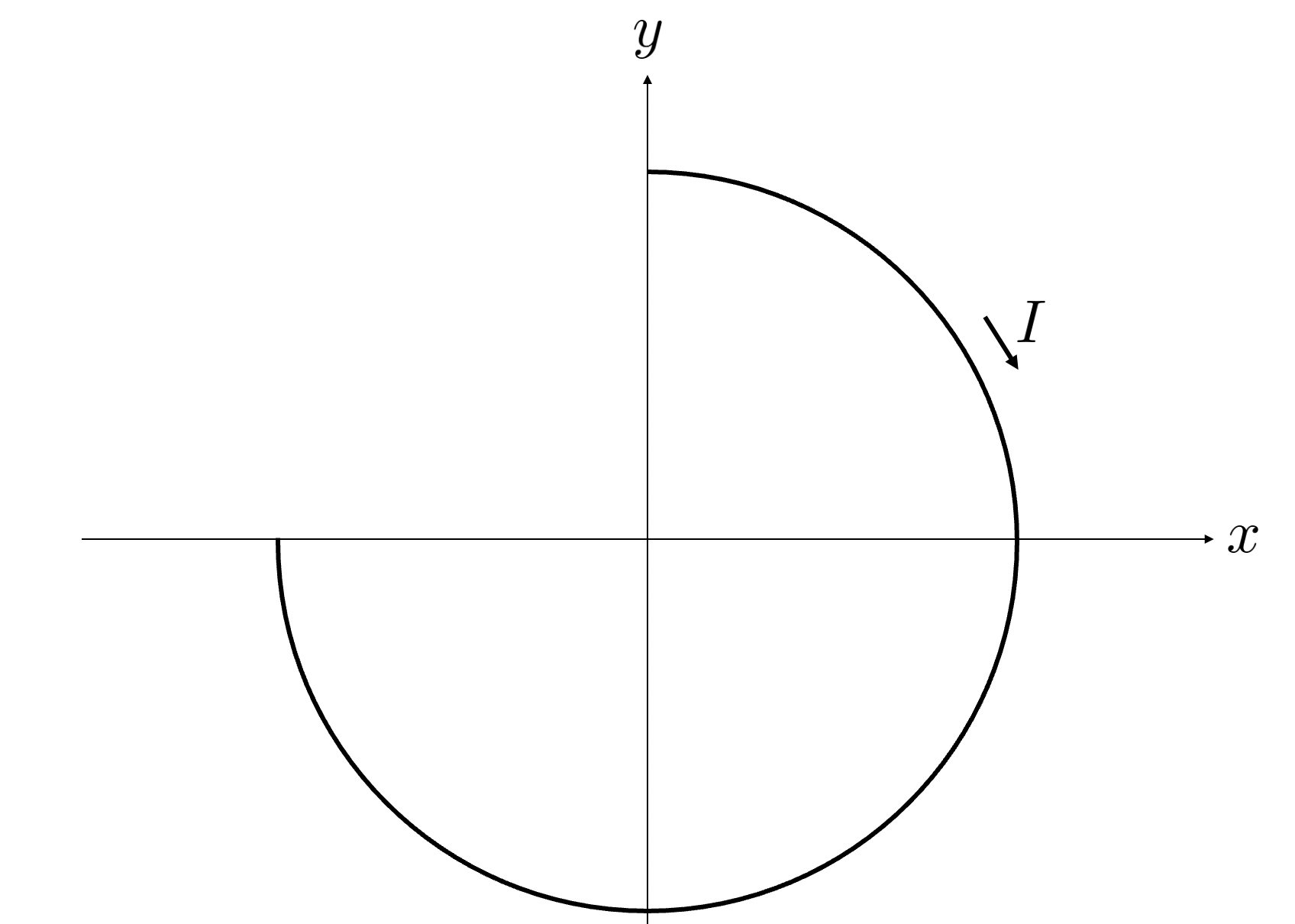
완벽한 원이 아닌 3/4 짜리 반지름이 $R$인 원에 전류가 시계방향으로 흐르고 있을 때, 이 도선이 원점에 만드는 자기장의 세기와 방향을 구해봅시다.
비오-사바르의 법칙은 적분식이라서 이를 구하기 위해서는 미소 전류를 생각해야 합니다.
그림을 다음과 같이 그리면

쉽게 알 수 있습니다. 아주 작은 막대 $dl$을 그림으로 그리고, 내가 원하는 지점으로부터 작은 막대 까지의 거리는 원의 반지름과 같으므로 $R$이죠. 그리고 작은 막대에 흐르는 전류는 $I$입니다.
그리고 방향을 생각해볼 수가 있는데, 전류가 만드는 자기장의 방향은 $d\vec{l} \times \hat{R}$로 정의됩니다. 따라서 빨간색 화살표와 초록색 화살표의 외적을 해주면 되므로 오른 나사 법칙을 이용하면 원점에 생기는 자기장의 방향은 지면으로 들어가는 방향입니다.
작은 막대 하나가 만드는 자기장의 방향을 구했는데, 이 작은 막대를 저 곳 말고 원의 아무곳이나 생각하더라도 항상 지면으로 들어가는 방향의 자기장을 만듭니다. 즉 작은 막대 하나가 만드는 자기장을 모조리 더해 3/4 원이 만드는 자기장을 구하더라도 그 방향은 동일하다는 것이죠.
자기장의 크기는 이렇게 구합니다.
$$ \vec{B} = \frac{\mu_0}{4\pi} \int \frac{I d\vec{l} \times \hat{r}}{r^2} $$
이 때 무엇에 대해 적분하고, 적분 범위는 어디부터 어디까지인지를 생각해야 하는데, 작은 막대의 길이로 적분을 하는거라서 결국 적분이 완료되고 나면 총 길이가 나와야 합니다. 여기서는 원을 따라가며 적분하기 때문에 결국 원의 총 둘레의 3/4이 나오게 됩니다. 따라서
$$ \vec{B} = \frac{\mu_0}{4\pi} \frac{I \cdot \frac{3}{4} \cdot 2 \pi R}{R^2} \hat{\otimes} = \frac{3\mu_0 I}{8R} \hat{\otimes}$$
로 정리할 수 있습니다. 여기서 $\hat{\otimes}$는 지면으로 들어가는 방향이라고 제가 표기하였습니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 속이 찬 공 모양 전하 (A Spherically Symmetric Charge Distribution) (0) | 2022.06.18 |
|---|---|
| 점전하에 의한 플럭스 (Flux Due to a Point Charge) (0) | 2022.06.18 |
| 전기장이 0이 되는 지점 찾기 (2) | 2022.06.05 |
| 쿨롱의 법칙을 이용한 전기력의 계산 (3) (5) | 2022.06.03 |
| 쿨롱의 법칙을 이용한 전기력의 계산 (2) (2) | 2022.05.29 |





