설군의연구소
전기장과 전기 퍼텐셜의 관계 본문
안녕하세요, 설군입니다.

전기 퍼텐셜 에너지에 대해서 먼저 기억해봅시다. 전기장이 펼쳐진 공간에서, 멀리 있는 전하 하나를 잡아 조심히 내가 힘을 주어 끌어올때, 전기장에 거슬러서 내가 그 전하에게 해준 일이 바로 전기 퍼텐셜 에너지입니다. (일이니까 에너지죠)
즉 전기력을 마이너스 부호를 붙여 거리로 적분해준 것입니다. (일이니까 힘과 거리의 적분입니다)
이 전기 퍼텐셜 에너지를 그 전하의 전하량으로 나누어 준 것이 그 전하가 가지는 전기 퍼텐셜 입니다. 즉, 힘과 거리의 적분을 전하량으로 나누어준 것입니다. 그런데 힘이라는건 전기력이었으니까, 전기력을 전하량으로 나누어 준것은 전기장입니다. 즉 전기 퍼텐셜은 전기장과 거리의 적분이 됩니다.
전기 퍼텐셜은 전기장을 거리로 적분한 것이다. 그렇다면 전기장은 전기 퍼텐셜을 거리에 대해 미분해준 것이 됩니다.
이를 표현하면 다음과 같습니다.
$$ \begin{split} V = & = \int dV = -\int \vec{E} \cdot d\vec{s} \\ dV =& - \vec{E} \cdot d\vec{s} \end{split} $$
전기 퍼텐셜은 전기장을 거리로 적분한 것이므로 위와 같이 쓸 수 있고, 만약 전기장이 $x$방향만 존재한다고 생각하면? $ \vec{E} \cdot d\vec{s} = E_x \cdot dx$가 됩니다. 따라서 위의 식은 $dV = -E_x \cdot dx$가 되고, 이를 다시 표현하면
$$ E_x = - \frac{dV}{dx} $$
와 같이 표현됩니다. 위에서 언급했던 것처럼 전기장은 전기 퍼텐셜을 거리에 대해 미분해준 꼴로 표현됩니다.
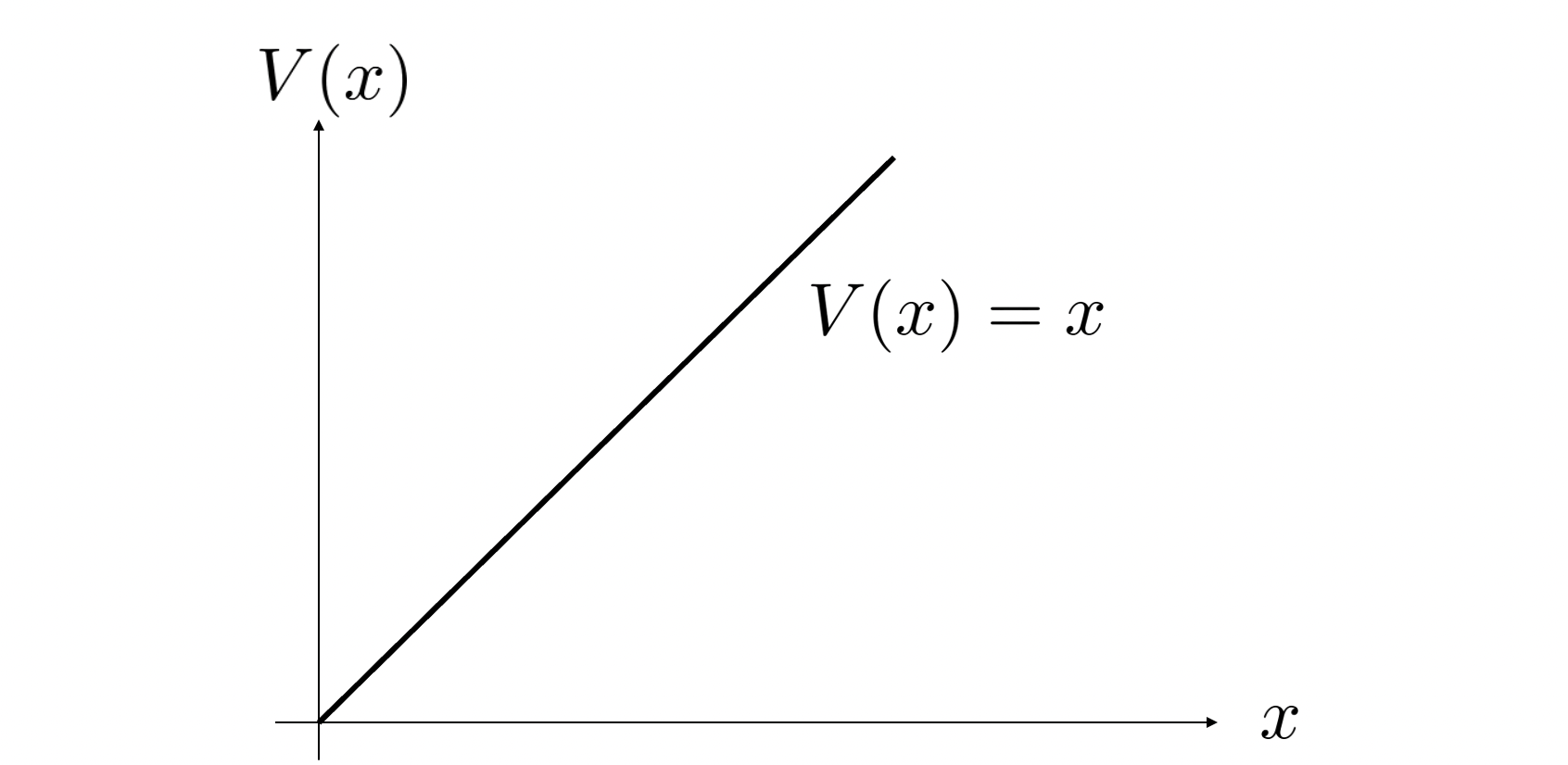
만약 퍼텐셜이 $V(x) = x$와 같이 $x$에 관한 일차 함수라고 생각합시다. 즉 일차원 좌표에서 오른쪽 방향을 $+x$방향이라고 할 때, 오른쪽으로 갈 수록 전기 퍼텐셜이 점점 높아지는 상황입니다. $x=0$에 있는 양전하가 가지는 전기 퍼텐셜 에너지는 작고, $x=1$에 있는 양전하가 가지는 전기 퍼텐셜 에너지는 더 크고, $x=2$에 있는 양전하가 가지는 전기 퍼텐셜 에너지는 더 더 크고... 이렇게 되는 상황이죠.
이런 경우에 전기장 $x$가 커질 때 어떻게 될까요? 미분해보면 전기장을 구할 수 있습니다.
$$ E_x = -\frac{dV}{dx} = - \frac{d}{dx} (x) = -1 $$
즉, 전기장은 상수값으로 $-1$입니다. 전기장의 $x$성분이 $-1$이라는 뜻이므로, 전기장은 $\vec{E} = -1 \hat{x}$라는 뜻입니다. 즉 전기장은 $-x$방향으로 일정한 세기로 펼쳐져 있는 상황입니다.
퍼텐셜은 오른쪽으로 갈 수록 커졌었죠? 즉 양전하가 가지는 전기 퍼텐셜 에너지가 오른쪽으로 갈수록 점점 커졌었습니다. 마치 언덕의 경사가 올라가는 것처럼요. 만약 양전하를 임의의 곳에 놓는다면, 그 양전하는 또르르 굴러 전기 퍼텐셜 에너지가 작아지는 지점으로 자연스럽게 전기력을 받아 가속할 것입니다. 자연은 퍼텐셜 에너지가 낮아지는 방향을 선호하게 되니까요. 그런데 이걸 앞서 구한 전기장과 연관시켜 보면, 전기장의 방향이 $-x$방향이므로 양전하가 왼쪽으로 힘을 받아 이동한다는 것으로도 설명이 가능합니다.
지금은 $x$축에 대해서만 생각했지만 일반적인 방향에 대해서도 성립합니다. 또한 점전하와 같이 전기장을 구 형태로 쭉 뻗어가도록 만드는 상황이라거나, 양전하와 음전하가 같이 존재하는 상황이어도 모두 다 위의 관계(전기장은 전기 퍼텐셜의 거리 미분 이라는 관계)를 만족합니다.
$$ E_x = -\frac{\partial V}{\partial x} \quad E_y = -\frac{\partial V}{\partial x} \quad E_z = -\frac{\partial V}{\partial z} $$
이렇게도 표현할 수 있어요. 아주아주아주 일반적으로는 그래이디언트 라는 기호를 이용해서, 직교 좌표계 뿐 아니라 구면 좌표계, 원통 좌표계에서도 사용할 수 있도록
$$ \vec{E} = - \vec{\nabla} V $$
로 표현하기도 합니다. (일반물리학보다 더 심화된 내용의 전자기학 책을 보면 이렇게 표현합니다.)
* 참고로 그래이디언트 를 기울기 라고 우리말 용어로 말하곤 하는데, 아까 퍼텐셜 이라는 언덕을 따라 양전하가 굴러 내려오는 것처럼, 마치 퍼텐셜 이라는 언덕의 기울기가 전기장의 세기와 관련이 있다고 해석할 수 있으므로, 기울기 라는 용어도 참 좋은것 같아요. 기울기가 급하면(경사가 급하면) 전기장의 세기가 큰 것이죠.
또는 이렇게도 표현됩니다.
$$ \vec{E} = - \vec{\nabla}V = - \left( \hat{i} \frac{\partial}{\partial x} + \hat{j} \frac{\partial}{\partial y} + \hat{k} \frac{\partial}{\partial z} \right) V $$
* 예제
점전하가 만드는 전기장과 전기 퍼텐셜 사이의 관계를 생각해봅시다. 이 경우에 관계식은
$$ E_r = -\frac{dV}{dr} $$
입니다. $r$을 쓴 이유는, 점전하는 구의 형태로 온 방향으로 뻗어나가는 전기장을 만들기 때문입니다. 점전하가 만드는 전기 퍼텐셜을 식으로 쓰면
$$ V(r) = k \frac{q}{r} $$
로 쓸 수 있습니다. 이를 미분해주고 마이너스 부호를 붙여 주면 전기장을 구할 수 있습니다.
$$ E(r) = (-) \left( - k \frac{q}{r^2} \right) = k\frac{q}{r^2} $$
이렇게 나오는데, 이는 쿨롱의 법칙으로 곧바로 구한 점전하가 만드는 전기장 식과 (당연하게도) 동일합니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 고리 전하 분포가 만드는 전기 퍼텐셜 (0) | 2022.08.27 |
|---|---|
| 전기 쌍극자가 만드는 전기 퍼텐셜 구하기 (0) | 2022.08.06 |
| 여러 점전하가 만드는 전기 퍼텐셜 (0) | 2022.07.23 |
| 점전하에 의한 전기 퍼텐셜과 전기 퍼텐셜 에너지 (0) | 2022.07.16 |
| 홀 효과(Hall effect)와 양공 개념의 완벽한 이해 (일반물리학 수준) (0) | 2022.07.16 |





