물리 2 - 등속 원운동

안녕하세요, 설군입니다.

등속 원운동은 일정한 '속력'으로 원 궤도를 운동하는것입니다.
무한히 원 궤도를 운동한다고 생각해봅시다.

주기적인 운동이라는 걸 알 수 있습니다.
일정한 주기를 가지고 원을 한 바퀴, 두 바퀴... 이렇게 도니까요.
원을 한 바퀴 도는 데 걸린 시간을 주기라고 합니다. 다른 말로는, 제자리로 돌아오는 데 까지 걸린 시간입니다.
이 때 속력은 과연 어떻게 될까요?

원의 반지름을 \(R\) 이라고 하면, \( \text{(속력)} = \frac{\text{(이동거리)}}{\text{(시간)}} \) 이므로
이동거리는 원의 둘레니까 \( 2 \pi R \)이고, 그것을 시간인 \(T\)로 나누어주면됩니다.

즉, 반지름이 \(R\)이고, 주기가 \(T\)인 등속 원운동에서의 속력은
\(v = \frac{2\pi R}{T}\) 입니다.

그런데 원운동은 특이하게도 각속도라는게 존재합니다.
각속도는 사실 벡터 물리량인데, 각속도의 크기만을 각속력이라고 말합니다.
그래서 이제부터 각속력이라는 용어를 이용해서 설명해볼게요.

각속력은 일정한 시간동안 몇 도의 각도를 회전하느냐를 말합니다.
그럼, \(T\)라는 시간동안. 즉 한 주기동안은 \(360^\circ\)를 회전하겠죠. 그런데 각속도(각속력)단위에서 도를 채용하지 않고 rad(라디안)을 채용합니다.
따라서 \(2\pi\) 만큼의 각도를 돌겠죠.

각속도는 각도 나누기 시간 이므로 \( \frac{2\pi}{T} \)가 바로 등속 원운동에서의 각속도가 됩니다. (각속력)

$$ \begin{split} & \text{반지름}: R, \text{주기}: T \\ &\text{속력} \ v= \frac{\text{(이동거리)}}{\text{(시간)}} = \frac{2\pi R}{T} \\ &\text{각속력} \ \omega = \frac{2\pi}{T} \\ &\therefore v=R\omega \end{split}$$

이렇게 \(v=R\omega\)라는 식도 성립하게 됩니다. (문제 해결할 때 유용하게 쓰입니다.)
구심 가속도는 원 궤도의 중심 방향으로 작용하는 가속도라는 뜻입니다.
등속 원운동은 순간 속도의 방향이 계속 변하는 운동입니다.
비록 속도의 크기 즉 속력은 변하지 않지만 방향은 계속 변하므로 가속운동이라는 것이죠

가속도가 존재한다는 뜻인데, 그 가속도의 방향은 원의 중심 방향입니다.
그 가속도의 크기를 바로 구심 가속도의 크기라고 하고, \( a \) 라고 씁니다. 각가속도라는 개념도 있는데 그거랑 다른 개념입니다.
그 크기는 \( a = R\omega^2 \)으로 나타냅니다.

또한 기본적으로 주기는 진동수의 역수이므로, \( T = \frac{2\pi}{\omega} \) 이고, \( f = \frac{1}{T} = \frac{\omega}{2\pi} \)입니다.

달이 지구를 도는 운동을 등속 원운동이라고 생각하고,
달이 등속 원운동할 수 있게 해주는 구심력을 지구와 달 사이의 만유 인력이라고 생각해봅시다
그 궤도의 반지름은 \(R\), 지구와 달의 질량은 각각 \(M\)과 \(m\)으로 놓고 생각해보면 됩니다.

$$ \begin{split} \text{(만유인력)} &= \text{(구심력)} \\ G \frac{Mm}{R^2} &= ma \ (a: \text{구심 가속도(등속 원운동 이니까))} \\ G \frac{Mm}{R^2} &= m \frac{v^2}{R} \\ v^2 &= \frac{GM}{R} \\ \therefore v &= \sqrt{\frac{GM}{R}} \end{split} $$

이렇게 달 이라는 물체에 대해서 \( F=ma \) 를 적용해서
\( \text{(만유인력)} = \text{(구심력)} = ma  \) (\(a\)는 구심 가속도) 라는 식만 세우면
쉽게 그 원운동의 속력 \(v\)를 구할 수 있습니다.

그런데 여기서 식을 조작해보면
\(a\)는 아까 \(R\omega^2\)으로 나타낼 수 있다고 했고(구심가속도)
그것에다가 \(\omega = \frac{2\pi}{T}\)이므로 주기 \(T\)에 대해 나타낼 수 있으므로
주기를 구할 수 있습니다.

동시에, 케플러 법칙 중 조화의 법칙을 이용해봅니다.

$$ \begin{align} G\frac{Mm}{R^2} &= ma = mR\omega^2  \\ &\ \ \ \ \ \ \ \ \left( \omega =  \frac{2\pi}{T} \right)\\ &= mR \frac{4\pi^2}{T^2}\\ T^2 &= \frac{R^2}{GMm} mR\cdot 4\pi^2\\ &= \frac{4\pi^2 R^3}{GM} \end{align} $$

케플러 제 3법칙: 조화의 법칙

$$ T^2 \propto a^3 $$

이 때, 비례 상수 \(k\)를 넣어 등식으로 만들면,

$$ T^2 = ka^3 $$

위의 만유인력으로부터 유도한 식과 비교하면, 비례 상수를 알 수 있다. 따라서,

$$ T^2 = \frac{4\pi^2}{GM} R^3 $$

이 때, 조화의 법칙에서의 \(a\)는 행성이 운동하는 궤도의 장반경을 말하는 것이므로, 행성이 원궤도를 운동하는 경우에는 장반경이 곧 반지름과 같다.

그러면 행성의 운동(여기서는 지구와 달)을 등속 원운동으로 생각했을 때

조화의 법칙에서 비례 상수 \(k\)값을 찾을 수 있습니다!

 

다음은 수능특강 문제입니다.

[7025-0003]
그림은 지구를 중심으로 등속 원운동 하는 위성의 이동 경로의 일부를 나타낸 것이다. 위성의 궤도 반지름은 \(r\)이고, 중심각이 \(60^\circ\)인 경로 상의 점 \(p\)에서 점 \(q\)까지 이동하는 데 걸린 시간은 \(t_0\)이다.

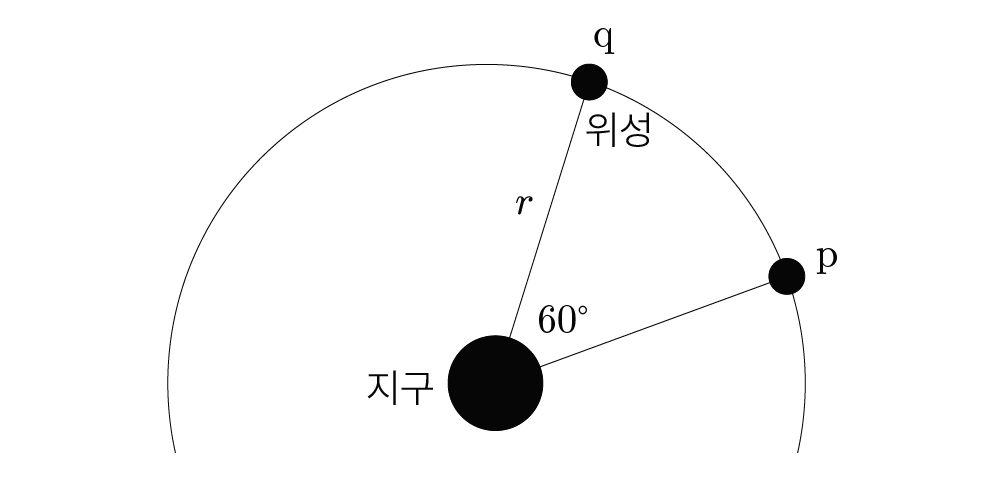
이에 대한 설명으로 옳은 것만을 <보기>에서 있는 대로 고른 것은?
<보기>
ㄱ. \(p\)를 기준으로 할 때, \(q\)의 위치 벡터의 크기는 \(r\)이다.
ㄴ. 순간 속도는 \(p\)와 \(q\)에서 같다.
ㄷ. \(p\)에서 \(q\)까지 평균 가속도의 크기는 \( \frac{\pi r}{3 t_0^2}\)이다.

하나씩 차근차근 보기를 풀어봅시다.

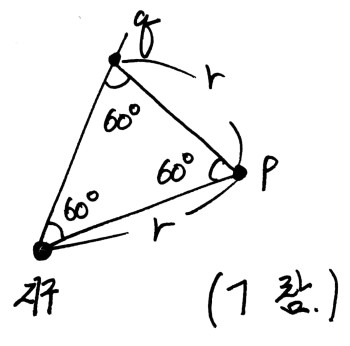
p점을 기준으로 바라본 q의 위치벡터는 p에서 q로 가는 벡터를 그리면 됩니다.
문제에서 60도라고 했으므로 정삼각형이고, 그 위치벡터의 크기는 \(r\)이라는걸 알 수 있으므로 ㄱ은 맞는 말이 되네요.

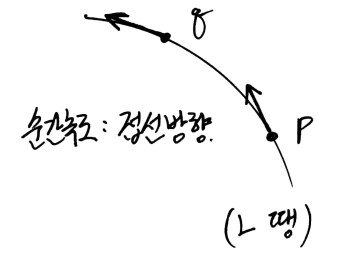
등속 원운동에서 순간 속도는 매 순간의 접선 방향입니다. 따라서 등속 원운동에서 매 순간 속도는 다 다르죠.

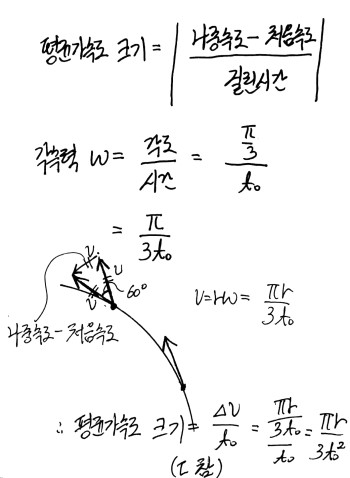
평균 가속도의 정의는 \( \text{(평균 가속도)} = \frac{\text{(나중 속도)} - \text{(처음 속도)}}{\text{(걸린 시간)}}입니다.

그런데 크기를 물어보았고, 속도는 벡터이므로

속도의 변화를 구할때에는 벡터 셈으로 계산해주어야 합니다.

먼저 문제에서 주어진 조건으로는 각도 \(60^\circ\)를 도는데 \(t_0\)의 시간이 걸렸다고했으므로 그 동안의 각속력 \(\omega\)를 구할 수 있고요

속도의 변화를 알기 위해 벡터를 그려보면 \(60^\circ\)인데, p점에서의 속력과 q점에서의 속력이 같으므로

그 차도 같습니다. 정삼각형을 이루겠네요.

따라서 평균가속도의 크기 공식에 대입해서 풀어보면 ㄷ은 참이라는 걸 알 수 있습니다.

 

등속 원운동은 잘 알아놓아야 합니다.

2단원에서 전자기 부분에서 자기장에서의 대전입자의 운동에 원운동이 나오는데 그 때도 등속 원운동 개념을 이용하니까요.