설군의연구소
물리 1, 물리 2를 할 때 알아두면 좋은 것 1. 벡터의 개념 본문
안녕하세요, 설군입니다.
벡터를 잘 알아두면 물리학 문제를 풀때 편합니다. 그리고 대학 일반물리학에서도 잘 사용되고요.
1편에서는 벡터의 개념에 대해 다룰것이고
2편에서는 벡터의 덧셈, 뺄셈, 실수배
3편에서는 벡터의 곱셈(스칼라곱과 벡터곱)
4편에서는 벡터의 분해
5편에서는 벡터를 물리 문제에 접목시켜 풀어보는 걸 해보겠습니다.
이 편(1편)에서는 벡터의 개념, 스칼라와 벡터의 차이, 벡터라는 건 크기와 방향을 가지고있다, 벡터는 좌표에 옮길 수 있다, 벡터의 크기는 피타고라스의 법칙으로 구할 수 있다, 단위벡터라는 게 있다, 단위벡터를 이용해서 벡터를 성분화시킬 수 있다(성분벡터) 등에 대해 다룹니다.

벡터는 크기와 방향을 가지고 있는 물리량입니다.
우리가 흔히 일상생활에서 말하는 '양'에 관련된 건 보통 크기만 가지고있습니다.
사람이 4명이다. 물이 10 L있다. 감자가 4 kg있다. 여기서 4 명, 10 L, 4 kg은 모두 스칼라라고 합니다.
왜냐하면 방향이 없고 크기만 있기때문이죠.
그럼 방향과 크기를 같이 가지고있는 물리량은 대체 무엇이냐? 대표적으로 속도와 힘이 있습니다.
어떤 자동차가 동쪽으로 4 m/s로 달리고있다. 철수가 상자를 북서쪽으로 10 N의 힘으로 밀었다. 여기서 동쪽으로 4 m/s, 북서쪽으로 10 N은 모두 방향과 크기를 가지고있는 벡터량이지요.
특히나 벡터는 방향이라는 중요한걸 가지고있기때문에
단순한 문자로 표현하기가 번거롭습니다. 위처럼 '북서쪽으로 10 N'이렇게 전부 다써주긴 귀찮죠.
그래서 만든 벡터의 표시법이 있습니다. 간단하게 눈으로 보기 편한것은 화살표를 이용한것이고
계산할 때 편리하게 하기 위한것은 성분벡터입니다.

벡터는 이렇게 그릴 수 있고 각각의 명칭도 있습니다.
벡터의 시작부분은 시점이라고 하고, 벡터의 화살표 즉 뾰족한 부분은 종점이라고 합니다.
꼬리와 머리라고 해도 좋고요.
그리고 벡터가 여러 개 있을 때에는 헷갈리지 않기 위해서 화살표 위에 벡터의 이름을 적어줘야죠
A, B, C 등으로 적는데 굵게, 기울여서 적기도 하고
알파벳 위에 화살표를 붙여서 적기도 합니다.

이들은 모두 다른 5개의 벡터인것이죠.
벡터는 또한 평행이동이 가능한데요
이것은 무엇을 의미하냐면
어떤 두 벡터가 화살표의 길이가 같고 방향이 같을때
그 두 벡터는 같은 벡터인것입니다.
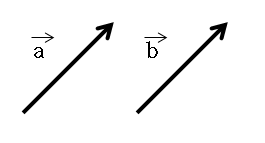
이렇게 두 벡터 a, b는 같은 벡터인것이죠.
벡터 a를 평행이동 시킨 게 벡터 b와 같죠
벡터는 좌표 평면으로 옮길 수 있습니다.
좌표 평면은 흔히 x, y좌표라고 하지요

이렇게 옮길 수 있습니다.
(벡터위에 알파벳 표기는 하지 않았습니다.)
이 벡터의 경우 가로 길이가 6, 세로 길이가 3이라고 생각하면 되는데요.
이것을 각각 이 벡터의 x축 성분(x성분), y축 성분(y성분)이라고 하기도 합니다.
성분을 표시한것을 바로 성분 벡터라고 하는데요
저 벡터의 알파벳이 A라고 치면
A=(6,3) 이렇게 표시하는것이 바로 벡터를 성분벡터로 표시하는것입니다.
(반드시 단순히 A라고 하면 안되고, 벡터표시를 해주어야합니다.

이렇게요)
다른 벡터를 봅시다.

A라는 벡터는 이렇게 옮길 수 있는데
이렇게 옮기면 본격적으로 벡터의 크기를 구할 수 있습니다.
벡터를 빗변으로 하는 직각삼각형을 만들어서 그 직각삼각형을 이용하면 됩니다.
동시에 피타고라스의 법칙을 이용하면 빗변의 길이를 구할 수 있듯이
벡터의 길이를 구할수 있는것입니다
(벡터의 길이 = 벡터의 크기)
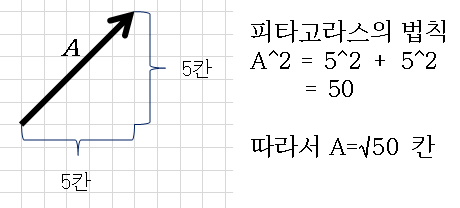
구하면 벡터의 크기가 나오죠.
벡터의 크기를 표기할 때에는 사실

이렇게 절댓값 표시를 해줘야하는게 원칙입니다!
위의 A=(3,6)이라는 벡터의 크기도 구할 수 있겠죠?
재미있는 벡터로는, 영벡터라는 게 있는데
말 그대로 0인것입니다. 이것은 벡터의 덧셈(뺄셈)에서 자연스럽게 나오는것이고
영벡터는 물리학 문제를 풀면서 크게 중요한 건 아닌 것 같아요.
단위벡터는 단위가 되는 벡터라고 생각할 수 있는데요
단위벡터는 자기가 옮겨놓은 좌표의 각 축에 해당하는 벡터가 있습니다.
이를테면 x, y평면에 벡터를 옮길 때에는 단위벡터가 x단위벡터, y단위벡터가 있는것입니다.


단위벡터는 벡터의 실수배를 알아야 사용할수있기도 합니다.
단위벡터를 이용하면 벡터를 성분을통해 나타낼 수 있습니다.
위의 A=(3,6)이라는 벡터를

으로 나타내는것이 그 방법입니다.
다음 편에서 봅시다!
(지속적으로 잘못된 내용은 고치고, 보완할 내용도 집어넣고 글을 다듬는것도 하겠습니다.)

'물리학 > 고등물리학' 카테고리의 다른 글
| 운동 방정식으로 풀기 or 에너지로 풀기 (0) | 2020.03.10 |
|---|---|
| 벡터의 덧셈, 뺄셈 그리고 실수배 (0) | 2020.03.10 |
| 전기력과 전기장 - 전기장에 관하여... (0) | 2020.03.10 |
| 전기력과 전기장 - 전기력에 관하여... (0) | 2020.03.10 |
| 힘의 방향과 운동의 방향은 항상 같은 것이 아니다. (0) | 2020.03.10 |




