설군의연구소
움직 도르래 가속 운동 분석 본문
안녕하세요, 설군입니다.
움직 도르래에 대한 정보를 아무것도 모르는 상황에서, 가속도의 법칙과 역학적 에너지 보존 법칙을 이용해서 모든것을 유도해봅시다.
움직 도르래에 매달린 물체가 움직인 거리는, 고정 도르래에 매달린 물체가 움직인 거리의 두 배이고,
가속도도 움직 도르래에 매달린 물체가 두 배 라는 사실을 전혀 모른다고 생각하고 모조리 유도해봅시다.

위의 그림과 같은 상황을 생각해봅시다.
물체 A, B 가 있고 움직 도르래 ㄱ과 고정 도르래 ㄴ이 있습니다.
고정 도르래 ㄴ 은 천장에 실 r 로 매달려 있습니다. 이 실의 장력은 그냥 고정 도르래를 고정해주는 역할이므로 큰 의미가 없습니다.
실 p는 움직 도르래 ㄱ 을 빙 돌고, 다시 고정 도르래 ㄴ 을 빙 돌아서 물체 B와 연결되어 있습니다.
실 하나에서의 장력은 동일하므로 물체 B를 위로 끌어당기는 장력의 크기는 $p$ 라고 생각하겠습니다.
그리고 움직 도르래 ㄱ 에 물체 A가 매달려 있는데, 그 장력은 $q$ 라고 하겠습니다.
물체가 어느 쪽으로 가속도를 받고 있는지 모르는 상황이라고 생각해봅시다. 그리고 움직 도르래에 매달린 물체와 고정 도르래에 매달린 물체의 가속도의 크기가 같은지 다른지도 모르는 상황이라고 생각해봅시다.
먼저 A가 아래 방향으로 가속 운동 하는 상황이라고 생각해봅시다. 그 가속도의 크기는 $a$ 라고 해봅시다. 그렇다면 B는 위 방향으로 가속도를 받는 가속 운동을 할 테고, 그 가속도의 크기는 $b$ 라고 해 봅시다.
i) 물체 A가 아래로 가속 운동 한다고 생각하고, 물체 A 에 대해 운동 방정식 세우기

물체 A가 받는 힘은 아래 방향으로 지구가 잡아당기는 힘이 있고, 위 방향으로 실 q가 잡아당기는 힘이 있습니다. 가속도의 방향은 아래 방향이라고 생각하자고 했으므로, 식은
$$ 50 - q = 5a $$
로 적을 수 있습니다.
그리고 다음으로, 물체 B에 대해 운동 방정식을 세우는 게 아니라, 움직 도르래 ㄱ 에 대해서 운동 방정식을 세워봅시다.
ii) 물체 A가 아래로 가속 운동 한다고 생각하고, 움직 도르래 ㄱ 에 대해 운동 방정식 세우기
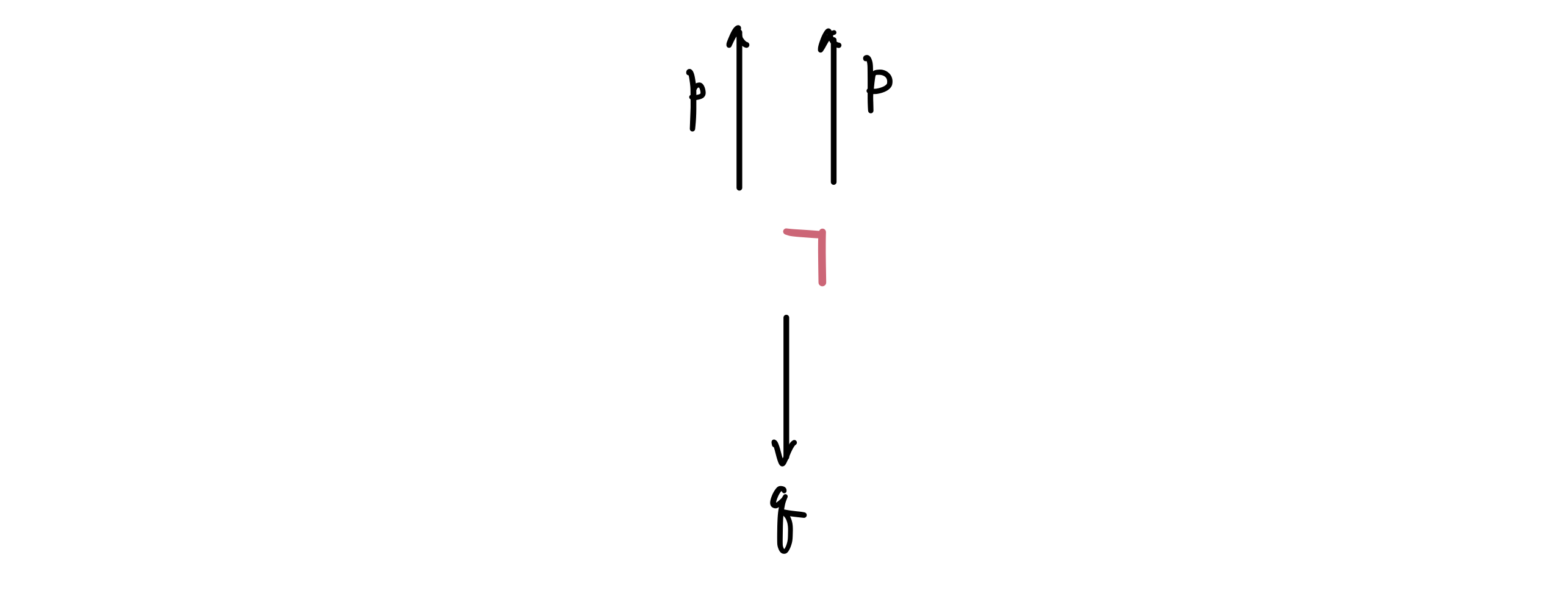
움직 도르래도 가속 운동을 할 겁니다. 그런데, 문제의 조건 중에 움직 도르래의 질량을 무시한다고 한다면, $F=ma$ 에 의해서, 움직 도르래 ㄱ 이 받는 알짜힘은 0과 같습니다. 질량을 0으로 생각할 수 있기 때문이죠.
따라서 그냥 장력의 관계식
$$ p + p = q $$
라는 정보를 얻을 수 있습니다.
iii) 물체 A가 아래로 가속 운동 한다고 생각 (B는 위로 가속 운동 한다고 생각) 하고 물체 B에 대해 운동 방정식 세우기
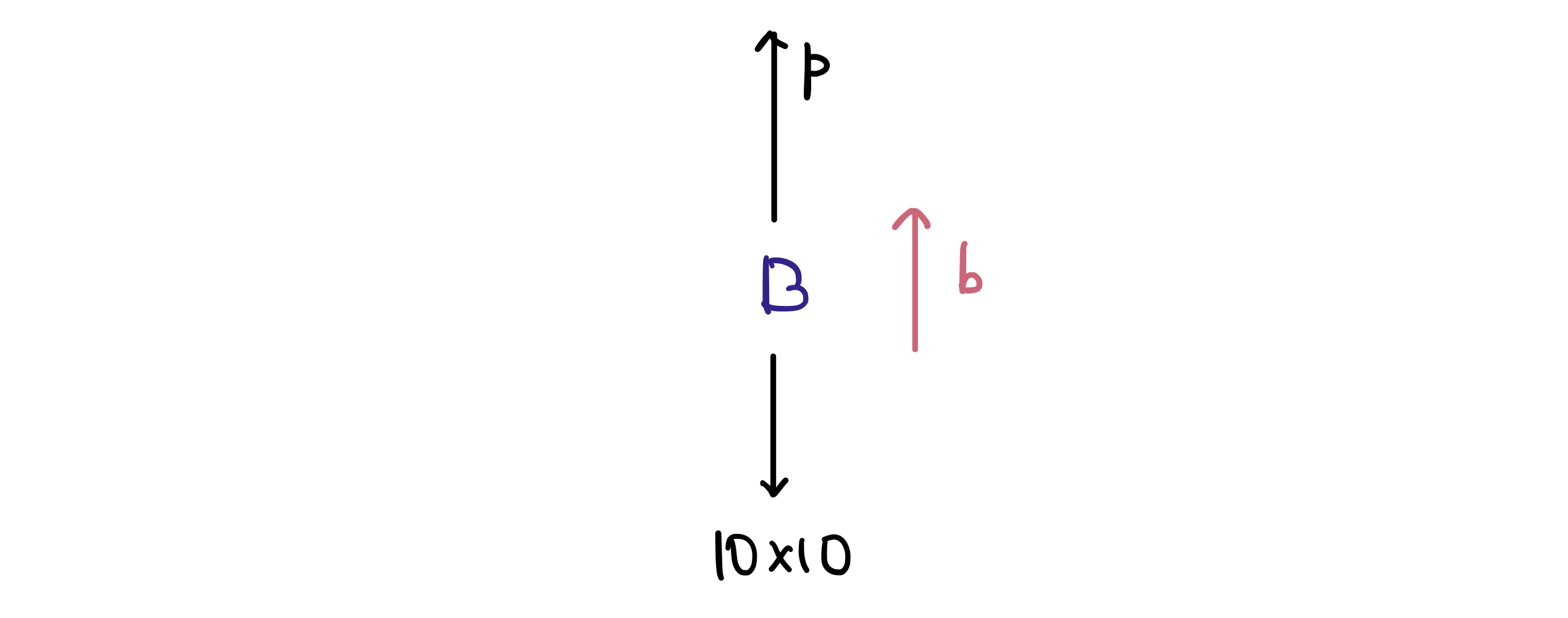
물체 B에 대해서도 똑같이 식을 세워주면,
$$ p - 100 = 10 b $$
라는 식을 얻을 수 있습니다.
이제 (i), (ii), (iii) 에서 얻은 세 식을 연립하여 정리해주면,
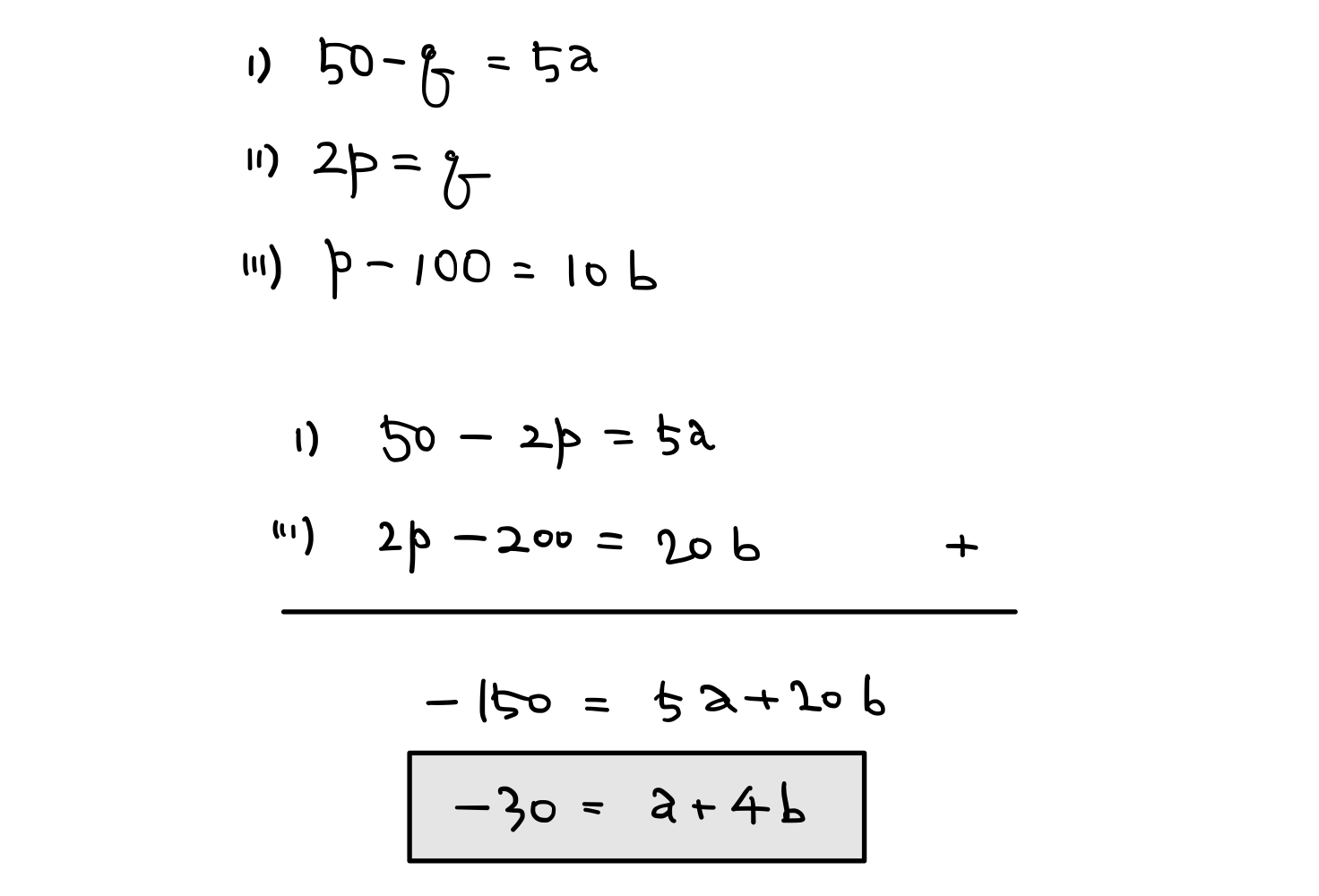
이런 식을 얻을 수 있습니다. 그런데 우리가 처음에 가정했을 때, 물체 A가 아래 방향으로 가속 운동 하는 가속도의 크기를 $a$ 라고 했고, 물체 B가 위 방향으로 가속 운동 하는 가속도의 크기를 $b$ 라고 했습니다. 가속도의 크기는 양수일 수밖에 없는데, 더해서 음수가 되어야 한다는 식이 나왔습니다. 즉 우리의 처음 가정이 모순이라는 의미입니다.
그럼 가속도의 방향이 반대가 되도록 상황을 생각해봅시다. 물체 A가 위 방향의 가속도로 운동 하는 상황이라고 놓고 다시 풀어봅시다.
그 과정은 다음과 같습니다.
* 이번에는 물체 A가 위로 가속 운동 한다고 생각 (물체 B는 아래로 가속 운동 한다고 생각)
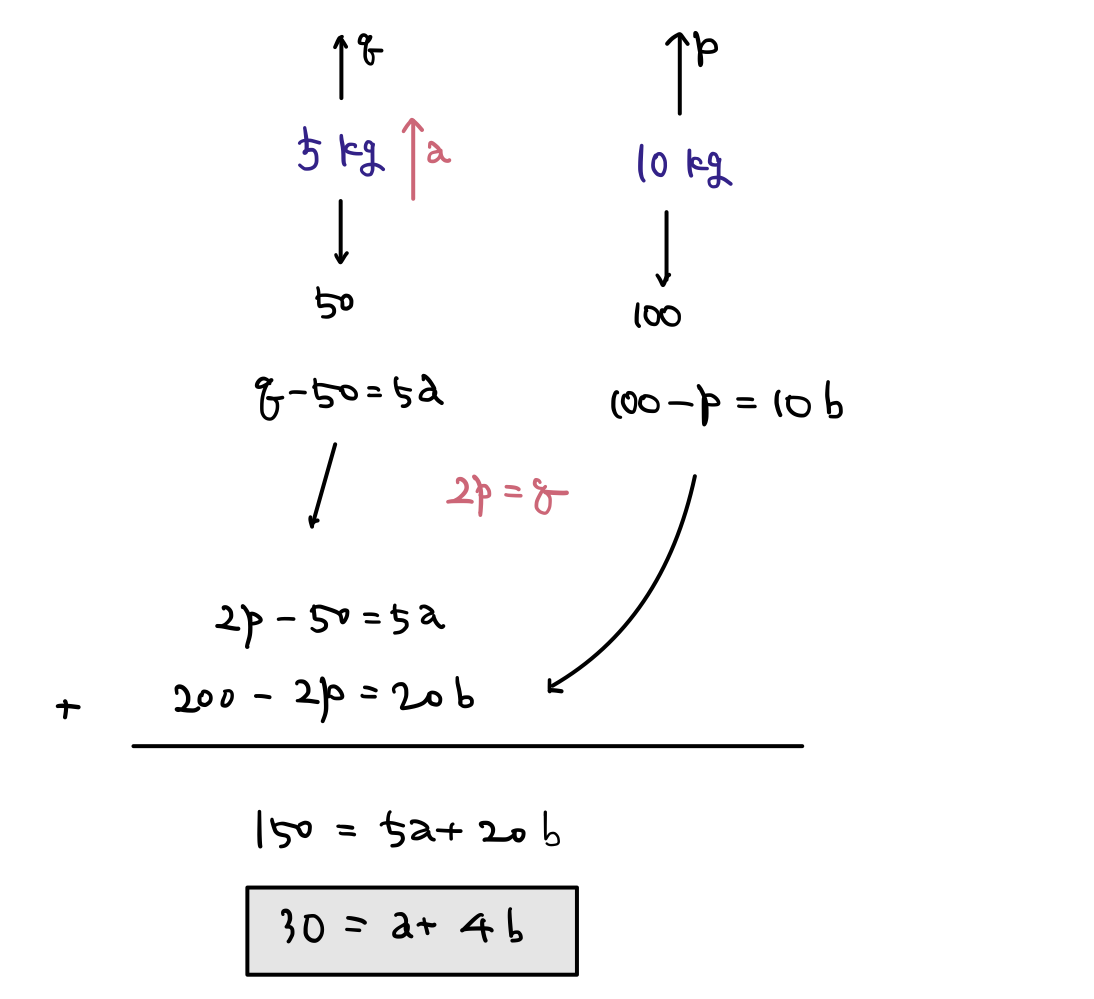
이번에는 말이 되는 것 처럼 식이 나왔습니다. 사실은 알고보면, 이전에 가정한 상황에서는 좌변의 부호가 음수였는데 이번에는 양수로 바뀐 것 밖에 없습니다. 즉, 가속도의 부호만 둘 다 바꾸어주면 되는거였습니다.
아무튼 이제 물체가 어느 방향으로 가속 운동해야 되는지는 정해진 것 같습니다. A가 위 방향으로 가속 운동을 해야겠네요.
* 가속도의 방향과 운동 방향이 동일하지는 않습니다. 예를 들어 가만히 있는 공을 내가 위로 던지면, 그 공의 운동 방향은 위쪽 방향이지만, 가속도의 방향은 아래 방향입니다.
* 그런데, 이 문제에서는 처음에 정지해있는 상황이었다고 생각하면, 가속도의 방향이 곧 운동 방향이라고 생각해도 됩니다.
따라서, A는 위로 실제로 움직이면서 속도가 점점 늘어나는 가속 운동을 한다고 봅시다.
이제 에너지적으로 분석을 해 봅시다. 물체 A의 역학적 에너지 변화량의 크기와, 물체 B의 역학적 에너지 변화량의 크기는 동일해야 합니다. (역학적 에너지 보존 법칙에 의해서 그렇습니다, 이에 대한 증명은 다른 글 주소를 첨부하도록 하겠습니다)
이때, 임의의 시간 $t$ 초 동안 물체 A가 위로 움직인 거리와, 그 때의 속력을 구해봅시다. 물체 A의 가속도가 $a$ 이므로, 등가속도 공식 중 두 번째 공식을 이용하면
$$ s = v_0 t + \frac{1}{2} a t^2 $$
이므로, 처음 속도 $v_0 =0 $ 이므로 대입해주면
$$ s = \frac{1}{2} a t^2 $$
만큼의 거리를 움직였습니다.
그리고 그 때 물체 A의 속력 $v$ 는
$$ v = v_0 + at $$
$$ v = at $$
가 되겠습니다.
그리고 물체 B는 아래로 움직일 테고, 같은 시간 $t$ 동안, 가속도는 $b$ 이므로 역시 구해보면 (이번에는 $d$ 의 거리를 움직였다고 해봅시다)
$$ d = \frac{1}{2} b t^2 $$
만큼의 거리를 움직였습니다.
그리고 그 때의 물체 B의 속력 $u$ (라고 하겠습니다) 는
$$ u = bt $$
가 됩니다.
역학적 에너지를 계산하기 위해서, 그림을 좀 더 제대로, 높이까지 표현해서 그려봅시다. 물체 A가 처음에 있던 위치를 지면으로 잡고, 물체 B가 처음에 있던 위치를 높이 $h$ 라고 하고 그림을 그리면 다음과 같습니다.
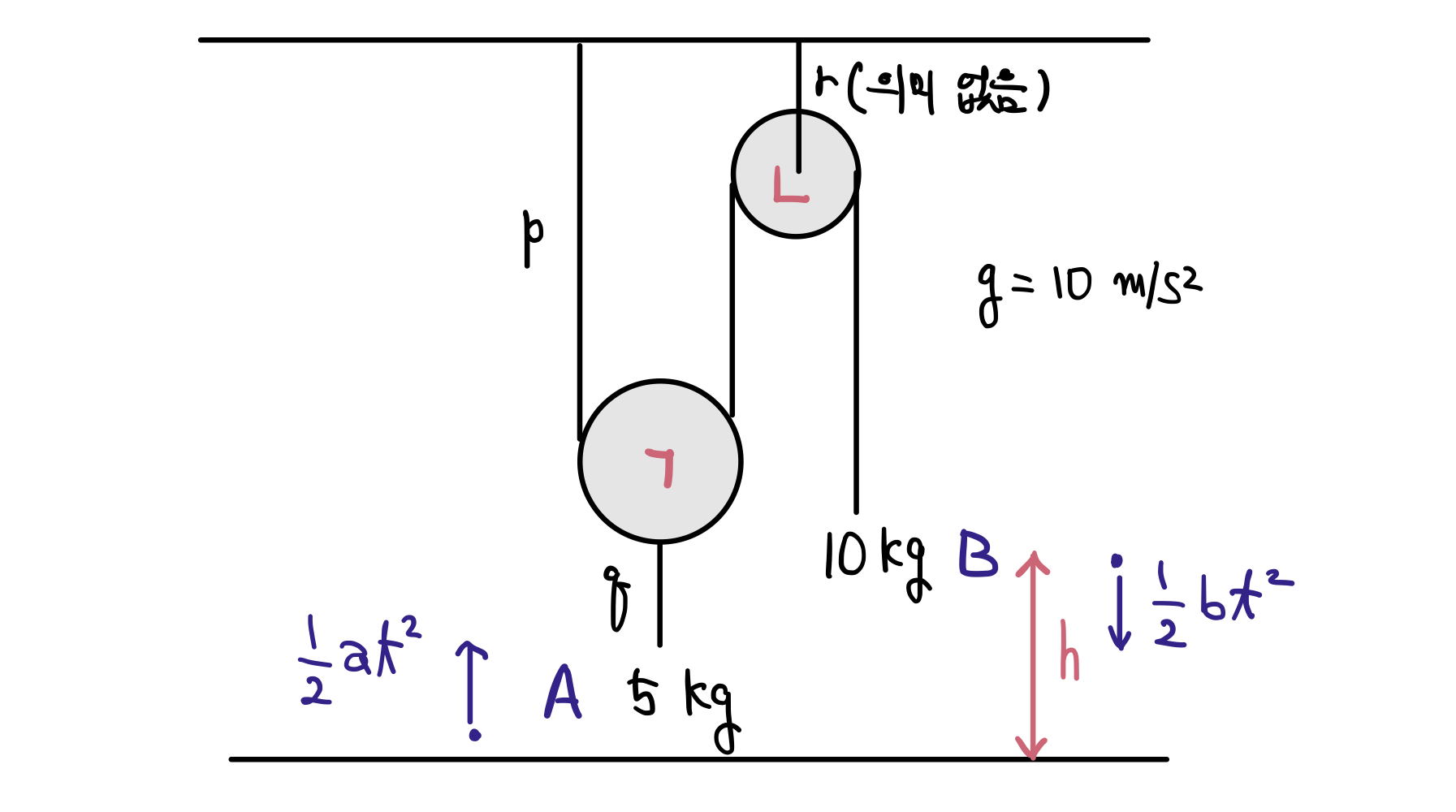
처음에 물체 A의 운동 에너지는 0 입니다.
처음에 물체 A의 퍼텐셜 에너지는 0 입니다.
처음에 물체 B의 운동 에너지는 0 입니다.
처음에 물체 B의 퍼텐셜 에너지는
$$ mgh = 10 \times 10 \times h = 100 h $$
입니다.
나중에 물체 A의 운동 에너지는
$$ K_\mathrm{A_f} = \frac{1}{2} \times 5 \times (at)^2 $$
입니다.
나중에 물체 A의 퍼텐셜 에너지는
$$ U_\mathrm{A_f} = 5 \times 10 \times \left( \frac{1}{2} at^2 \right) $$
입니다.
나중에 물체 B의 운동 에너지는
$$ K_\mathrm{B_f} = \frac{1}{2} \times 10 \times (bt)^2 $$
입니다.
나중에 물체 B의 퍼텐셜 에너지는
$$ U_\mathrm{B_f} = 10 \times 10 \times \left(h- \frac{1}{2} bt^2 \right) $$
입니다.
물체 A의 역학적 에너지 변화량은, (나중 역학적 에너지) - (처음 역학적 에너지) 이므로,
물체 A의 역학적 에너지 변화량은
$$ \frac{5}{2} a^2 t^2 + 25 at^2 $$
이 됩니다. 이 값은 양수입니다. $a$ 가 양수이기 때문입니다.
물체 B의 역학적 에너지 변화량도 같은 방법으로 계산하면,
물체 B의 역학적 에너지 변화량은
$$ \left[ 5 b^2 t^2 + 100 \left(h - \frac{1}{2} bt^2 \right) \right] - 100 h $$
입니다. 이 값은 양수인지 아닌지 모릅니다. $b$ 가 양수이긴 하지만요...
정리하자면, 각각 물체의 역학적 에너지 변화량은

이렇게 되는데, 역학적 에너지 보존 법칙에 의해서
물체 A의 역학적 에너지 변화량의 크기와, 물체 B의 역학적 에너지 변화량의 크기가 같아야 합니다.
물체 A의 역학적 에너지 변화량의 크기는, 저 값이 모두 양수이므로
$$ | \Delta E_{\mathrm{A}} | = \frac{5}{2} a^2 t^2 + 25 a t^2 $$
입니다.
물체 B의 역학적 에너지 변화량의 크기는, 절댓값을 씌워주게 되면 두 가지로 나뉘게 됩니다.
i)
$$ \Delta E_{\mathrm{B}} = 5b^2 t^2 - 50 bt^2 $$
ii)
$$ \Delta E_{\mathrm{B}} = 50bt^2 - 5b^2 t^2 $$
이렇게 나뉩니다.
(i) 의 경우로 생각해서, 둘의 크기가 같다고 놓고 풀어보면

두 가지 해를 구할 수 있는데, 두 경우 모두 물체 A의 가속도의 크기가 음수값이 나왔으므로 이것은 물리학적으로 말이 안 되는 경우입니다.
그럼 (ii) 의 경우로 생각해서 다시 풀어보면,

역시나 두 가지 해가 구해지는데, 이 경우에서는 물체 A의 가속도의 크기가 양수인 해가 존재하네요. 따라서 우리에게 맞는 해답은 마지막의 해,
$$ a = \frac{10}{3} \ \mathrm{m/s^2} $$
$$ b = \frac{20}{3} \ \mathrm{m/s^2} $$
입니다.
물체 A의 가속도의 크기가 물체 B의 가속도의 크기의 절반 이네요. 이 말은 곧
물체 A가 $x$ 만큼 이동할 때, 물체 B가 $2x$ 만큼 이동한다는 의미입니다.
이게 움직 도르래의 성질입니다. 이제 한 번 유도했으니 바로 써먹으면 됩니다.

'물리학 > 고등물리학' 카테고리의 다른 글
| 상대성 이론과 상대 속도 (0) | 2020.03.10 |
|---|---|
| 2017 수능특강 물리 1 36쪽 8번 도르래 문제 (0) | 2020.03.10 |
| 고정 도르래와 움직 도르래 (2) | 2020.03.10 |
| 일은 무엇인가? (0) | 2020.03.10 |
| 물리 2의 기본, 벡터의 분해를 알아보자 (0) | 2020.03.10 |




