설군의연구소
물리 2의 기본, 벡터의 분해를 알아보자 본문
안녕하세요, 설군입니다.
요즘 지식인 활동을 하며 답변을 하고 있는데요
제 답변을 하나 퍼 와서 블로그에 옮기겠습니다.
벡터의 분해를 설명하기 딱 좋은 문제가 있더라고요.
사실 이 문제는 답을 구하는 게 중요한 게 아니라 벡터를 분해할 줄 아는 게 중요하죠 ㅋㅋ
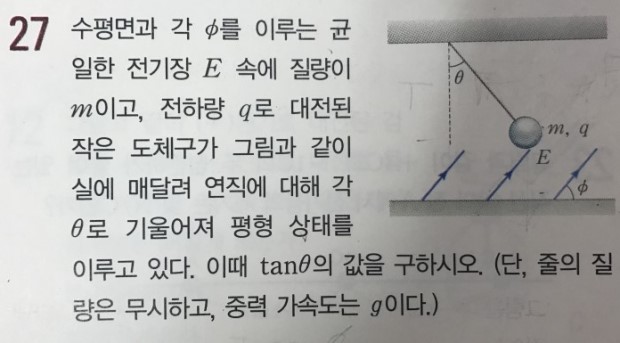
물리 1 문제는 아닌 것 같습니다.
왜냐면 힘을 벡터적으로 분해하는 것은 물리 1에서 묻지 않고 물리 2에서 묻기 때문입니다.
물체가 받는 힘을 분석해보면, 장력, 전기력, 중력이 있습니다.
물체가 정지해있으므로 이 힘들을 나름대로 방향을 따져서 더하면 0이 되어야 합니다.
힘을 분해해야 합니다.
힘을 분해할 때에는, x축 방향과 y 축 방향으로 분해해주시면 좋아요.
삼각비를 이용해서 삼각함수와 원래 힘의 곱으로 나타냅니다.

이렇게 각도 세타를 이루고 있는 F라는 벡터가 있다고 합시다.

이 F 벡터는, x 벡터와 y 벡터의 합으로 나타낼 수 있습니다.
이 x 벡터와 y 벡터가 무엇인지 찾는 것이 바로 벡터의 분해입니다.

쉽게 찾을 수 있습니다.
사인과 코사인의 정의에 의해서, x와 y를 F와 세타의 식으로 표현할 수 있습니다.
보통 x, y라고 놓지 않고

F의 x 성분이라고 해서 Fx
F의 y 성분이라고 해서 Fy
이렇게 놓습니다.
이제 문제로 돌아가 봅시다.
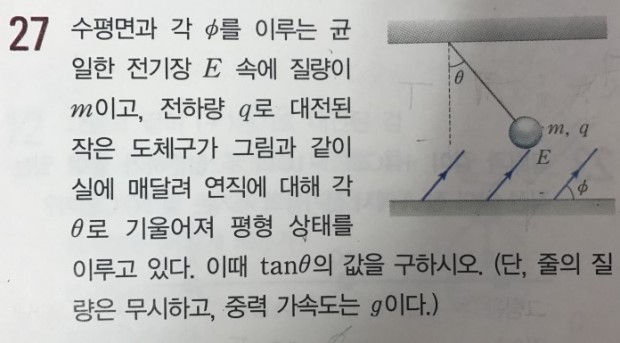
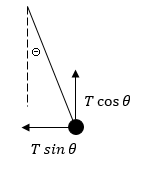
물체에 받는 장력을 분해해봤습니다.
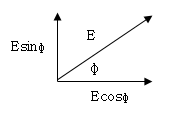
전기장을 분해해봤습니다.
물체가 받는 전기력은 전하량과 전기장의 세기를 곱해주면 됩니다.
따라서 물체는 qE의 전기력을 받습니다.
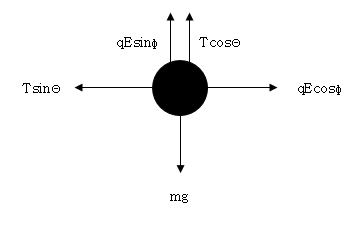
물체가 받는 모든 힘들을 표시해보면 이렇게 됩니다.
장력과 전기력은 원래 대각선 방향인데, 분해를 하고 난 후에는 x, y 방향만 받는 것으로 생각하면 됩니다.
물체가 정지해있으므로
x 방향의 힘은 합해서 0이고
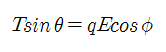
y 방향의 힘도 합해서 0입니다.
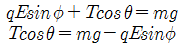
따라서 T사인 세타와, T 코사인 세타를 구했습니다.
탄젠트 세타의 정의는 코사인 세타가 분모, 사인 세타가 분자인 것이므로
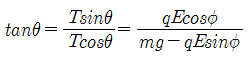
이렇게 구할 수 있습니다.
공부 파이팅 하시길 바랍니다.
다시 한 번 말씀드리지만, 물리 1 개념에서 벡터의 분해는 나오지 않아요.

'물리학 > 고등물리학' 카테고리의 다른 글
| 고정 도르래와 움직 도르래 (2) | 2020.03.10 |
|---|---|
| 일은 무엇인가? (0) | 2020.03.10 |
| 절벽에 매달린 물체의 무게에 의한 운동 분석 (0) | 2020.03.10 |
| 고정 도르래 하나에 매달린 물체의 운동 분석 (2) | 2020.03.10 |
| 2016년 11월 17일 시행 대학수학능력시험 물리 2 문제 9번 (0) | 2020.03.10 |




