설군의연구소
ㄷ자 도선에 걸친 금속 막대가 움직일 때 본문
안녕하세요, 설군입니다.
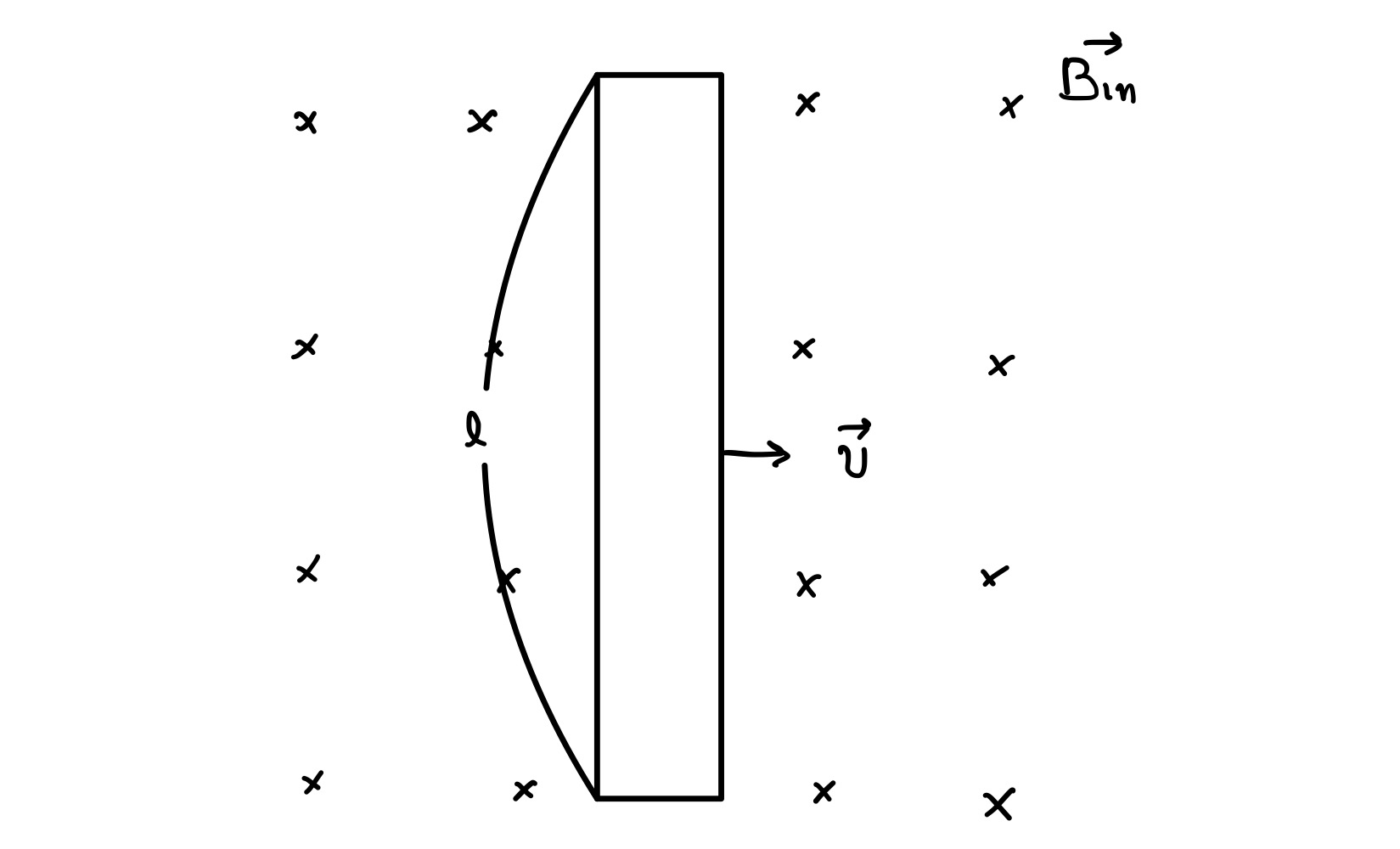
그림과 같이 화면을 뚫고 들어가는 방향으로 자기장 $\vec{B}_{\mathrm{in}}$ 이 펼쳐져 있습니다. 그곳에는 길이가 $l$인 금속 막대(두껍게 그렸음)가 있습니다. 이 금속 막대가 일정한 속도 $\vec{v}$ 로 오른쪽으로 움직이고 있는 상황을 생각해 봅시다.
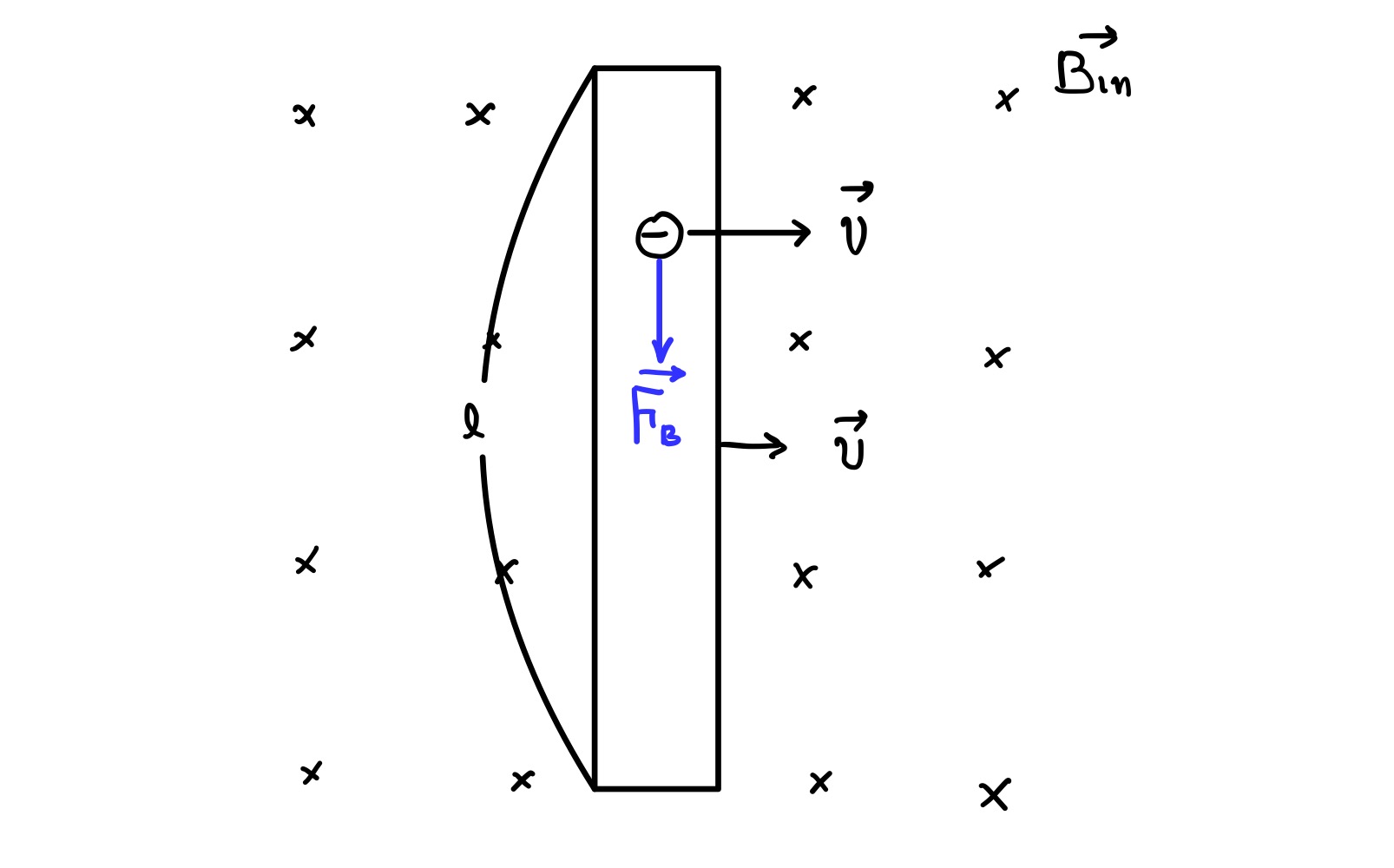
금속 막대가 오른쪽으로 움직이고 있으므로, 금속 막대 내의 전자도 오른쪽으로 움직이게 됩니다. 그런데, 자기장이 펼쳐진 공간에서 전하를 띤 입자가 움직일 때에는 자기력을 받습니다. 오른 손바닥 법칙을 이용하여 전자가 받는 자기력의 방향을 찾아보면, 그림에서 표시한 것처럼 파란색 벡터 방향입니다. 그 자기력의 세기와 방향을 $\vec{F}_{\mathrm{B}}$ 라고 표시했습니다.

금속 막대 내부에는 전자가 많이 있고, 그 전자들은 모두 자기력을 받아 금속 막대의 아래에 쏠리게 됩니다. 그러면 상대적으로 전자 수가 적어진 부분은 양전하를 띠게 되고, 전자가 쏠린 부분은 음전하를 띠게 됩니다. 그림에서 표시한 것처럼 막대의 윗부분은 양전하를 띠게 되고, 아랫부분은 음전하를 띠게 되는 것이죠.
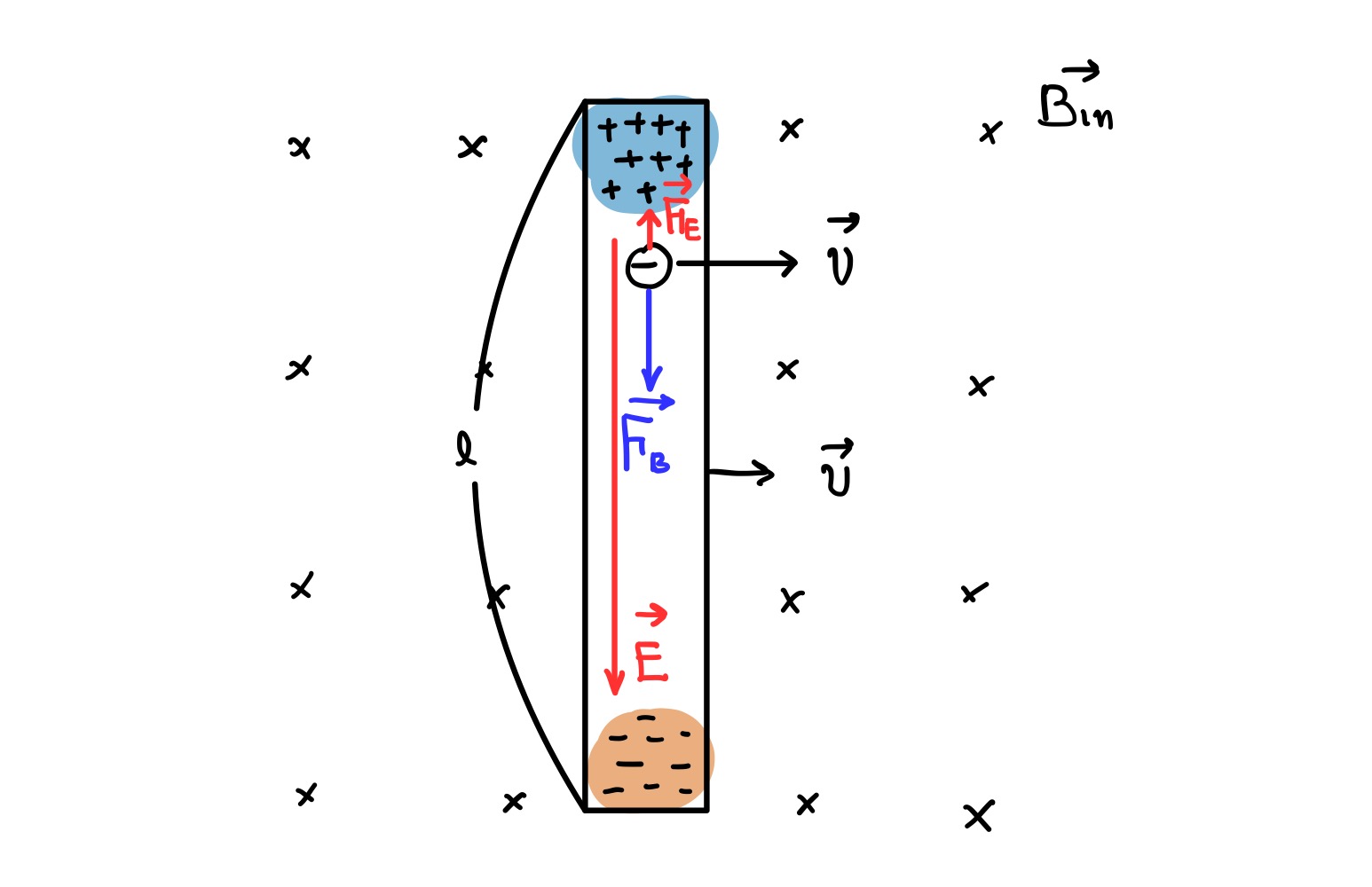
그렇게 되면, 쏠린 전하 분포에 의해서 금속 막대 내에 전기장이 펼쳐지게 됩니다. 전기장은 플러스 전하로부터 나와서 마이너스 전하로 들어가는 전기력선을 그리게 됩니다. 따라서 금속 막대에는 위에서 아래로 향하는 전기장(빨간 벡터로 표시)이 생기게 됩니다. 그러면 다시 금속 막대의 전자 하나에 대해서 생각해보면,

펼쳐진 자기장에 의한 자기력 $\vec{F}_{\mathrm{B}}$ 을 받게 되고, 전기장에 의한 전기력 $\vec{F}_{\mathrm{E}}$ 도 받게 됩니다.
만약 금속 막대가 오른쪽으로 움직이고 있는 상태에서, 더이상의 금속 막대 내부의 전자들의 위아래 이동은 없는 상황을 생각해봅시다. 그런 상황을 평형 상태라고 생각할 수 있어요. 따라서 금속 막대 내의 전자가 받는 알짜힘은 0이 됩니다. 따라서 전기력과 자기력이 평형인 상태입니다.
$$ \vec{F}_{\mathrm{E}} = \vec{F}_{\mathrm{B}} $$
전기장과 자기장의 세기, 전하를 띤 입자의 전하량과 속도를 알고 있을 때 그 입자가 받는 전기력과 자기력을 각각 풀어서 쓸 수 있습니다.
$$ qE = qvB $$
가 됩니다. 전하량 $q$ 를 소거해주면 $E=vB$ 의 식이 남게 됩니다. 이렇게 펼쳐진 자기장과 전기장, 그리고 막대를 움직이는 속력 사이에 관계식을 얻은 셈입니다.
다르게 말하면, 자기장이 펼쳐진 공간에서 금속 막대를 어떤 속도로 움직일 때, 전기장이 생긴다는 것이지요. 이 전기장은, 막대 위 아래로 전기 퍼텐셜 차이를 만든 것이라고도 할 수 있습니다. (전기장 = 전기 퍼텐셜의 차이에 의해 생김)
그 식을 다음과 같이 정리할 수 있습니다.
$$ \Delta V = El = Blv $$
전위차(전기 퍼텐셜 차이)가 위와 같이 자기장의 세기, 막대의 길이, 막대의 속력으로 결정되는 것입니다.
위의 상황에서는 금속 막대 하나에 대해서 생각했었습니다. 이 금속 막대가 ㄷ자 도선 위에 놓이게 되면 닫힌 회로를 만들게 되는데, 이 경우를 분석해봅시다.

그림과 같이 화면을 뚫고 들어가는 방향으로 균일한 자기장 $\vec{B}$ 가 펼쳐진 곳에, ㄷ자 금속 도선이 있습니다. 그 위에 금속 막대가 걸쳐 있습니다. ㄷ자 도선의 끝에는 저항 $R$ 이 달려 있고, 금속 막대의 길이는 $l$ 입니다. ㄷ자 도선의 끝에서부터 금속 막대까지의 거리는 $x$ 인데, 이 금속 막대를 내가 오른쪽 방향으로 $\vec{F}_{\mathrm{app}}$ 의 세기로 끌어당길 것입니다. 즉 $x$ 는 시간에 따라 바뀌는 물리량입니다. 이때, ㄷ자 도선에 금속 막대가 걸쳐 있으므로 이는 ㅁ자 도선(닫힌 도선)으로 생각할 수 있습니다. 금속 막대가 오른쪽으로 움직이면서 ㅁ자 도선의 넓이는 점점 넓어지는 것이죠.
고리 도선 입장에서는, 화면을 뚫고 들어가는 방향으로 자기력선이 점점 많아지게 됩니다. 렌츠의 법칙에 의해서 그걸 방해하는 방향으로 고리 도선은 자기력선을 만들어야 합니다. 즉 고리 도선은 화면을 뚫고 나오는 방향으로 자기력선을 만들어야 합니다. 따라서 고리 도선에는 유도 전류가 반시계 방향으로 흐르게 됩니다. 반시계 방향으로 고리 도선에 흐르는 유도 전류를 $I$ 라고 하겠습니다.
고리 도선을 통과하는 자기 플럭스를 물리량으로 표시하면 다음과 같습니다. 자기 플럭스는 자기장과 면적의 곱이라는 걸 생각해주면
$$ \Phi_{\mathrm{B}} = B \times lx $$
가 됩니다. 고리 도선의 면적은 가로와 세로의 곱이므로, 가로는 $x$ (즉 변하는 물리량) 이고, 세로는 $l$ 로 정해져 있으므로 둘을 곱해주면 됩니다. 자기장은 일정하다고 가정하고 있습니다.
렌츠의 법칙에 의하면, 자기 플럭스가 시간에 따라 변할 때 유도 기전력이 생기는데 이를 수식으로 표현하면 다음과 같습니다.
$$ \varepsilon = - \frac{d \Phi_{\mathrm{B}}}{dt} = - \frac{d}{dt} (Blx) = -Bl \frac{dx}{dt} $$
그런데, $\frac{dx}{dt}$ 는 막대 도선이 오른쪽 방향으로 변위가 시간에 따라 얼마만큼 변하느냐, 즉 막대의 속도를 말합니다. 따라서 그냥
$$ \varepsilon = -Blv $$
가 됩니다.
따라서 위에 그림의 오른쪽에 간략하게 그린 회로도와 같이, 위의 상황은 전압이 $ \varepsilon = Blv $ 인 건전지가 연결된 회로로 생각할 수 있습니다.
그래서 저항 $R$ 에 흐르는 전류의 세기는
$$ V = IR \rightarrow I = \frac{V}{R} = \frac{Blv}{R} $$
입니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 고리 도선이 자기장 영역을 통과할 때 (0) | 2024.02.03 |
|---|---|
| 임의의 곡선 모양 빗면에서의 물체의 운동 방정식 (1) | 2024.01.13 |
| 솔레노이드가 만드는 자기장 예제 (0) | 2023.12.16 |
| 물질이 나타내는 자성 (1) | 2023.11.18 |
| 직선 도선 주변에서의 자기 플럭스 구하기 (1) | 2023.10.14 |





