설군의연구소
저항, 비저항, 옴의 법칙 본문
안녕하세요, 설군입니다.

전류라는 개념을 배우기 전까지, 일반 물리학에서 도체를 공부할 때에는 도체 내부 전기장이 0인 상황을 공부하고 있었습니다. 전하의 이동이 더이상 없는 *정적 평형 상태*의 도체를 공부하고 있었던 것입니다. 하지만 도체 내부의 전기장이 항상 0인 것은 아닙니다. 도체 전선에 배터리를 연결하는 것 같은 상황이라면 도체 내부에도 전기장이 생길 수 있습니다. 이 경우에는 전하가 흐르게 되고 이것을 전류라고 합니다. 도체는 더이상 정적 평형 상태가 아니게 됩니다.
전류는 다음과 같이 임의의 지점에, 단위 시간당 전하가 얼마나 흘러가는지로 정의됩니다. 임의의 지점은 어떤 한 점일 수도 있고, 선일 수도 있고, 면일 수도 있어요. 이것에 대해 더 엄밀하게 정의하기 위해 전류 밀도라는 개념이 나중에 등장합니다. 일단은 전류의 정의부터 살펴봅시다.
$$ \text{(전류)} = \frac{\text{(전하량)}}{\text{(시간)}} $$
여기서 전하량이라는 건 임의의 지점을 지나가는 *총 전하량*을 말하는 것이므로, 여러 개가 지나간다면 전하의 개수도 생각해줘야 합니다. 그리고 전하들의 전하량이 만약 다르다면 각각의 전하량을 생각해줘야 합니다. 전하량이 1인 전하 5개와 전하량이 2인 전하 5개, 총 10개가 지나간다면, 지나가는 총 전하량은 15 인 것이죠. 그런데 이렇게 복잡하게 생각할 필요는 거의 없습니다. 보통 전류를 만드는 전하의 전하량은 모두 같은 경우가 많아서 그런 상황 위주로 생각합니다. 따라서 다음과 같이 나타냅니다.
$$ \text{(전류)} = \frac{\text{(전하의 개수)}\cdot \text{(전하량)}}{\text{(시간)}} $$
전하의 개수는 단순히 몇 개, 이렇게 표현하기보다는 주로 개수 밀도로 표현하곤 합니다. 개수 밀도는 다음과 같이 정의되므로,
$$ \text{(밀도)} = \frac{\text{(개수)}}{\text{(부피)}} $$
전하의 개수는 $ \text{(개수)} = \text{(밀도)} \cdot \text{(부피)} $ 로 정의됩니다. 따라서 전류는 다시
$$ \text{(전류)} = \frac{\text{(밀도)}\cdot\text{(부피)}\cdot e}{\text{(시간)}} $$
이 됩니다. 여기서 전하량은 간단하게, 모두 전자라고 생각하면 전자의 전하량 $e$를 대입할 수 있습니다.
단위에 대해서 잠시 생각해봅시다. 부피, 시간의 단위를 생각해 보아야 하는데요, 부피의 단위는 $\text{(길이)}^3$의 단위입니다. 그리고 시간의 단위는 분모에 있습니다. 부피 단위는 길이의 세제곱이므로, $\text{(길이)}^2 \cdot \text{(길이)} $ 로 쪼갤 수 있습니다. 따라서
$$ \text{(전류)} = \frac{\text{(밀도)}\cdot\text{(길이)} ^2 \text{(길이)} \cdot e}{\text{(시간)}} $$
이렇게 되는데, 여기서 분자의 길이 단위 하나와, 분모의 시간 단위를 생각해봐요. 이건 바로! 속력의 단위입니다. 따라서 전류는
$$ \text{(전류)} = \text{(밀도)} \cdot \text{(면적)} \cdot e \cdot v $$
이렇게 되고, 간단하게
$$ I = n A e v $$
이런 식으로 씁니다. 다시 말하지만 여기서 밀도는 개수 밀도를 말합니다. 부피 안에 몇 개의 전하가 들어있냐를 말해요.
그리고 다시 다음과 같이 *전류 밀도*라는 물리량이 정의됩니다.
$$ J = \frac{I}{A} = nev $$
정확히는 *부피 전류 밀도*라는 물리량입니다.
https://seolgoons.tistory.com/110
이전 글에서 다루었었는데, 전하들이 전기장에 몸을 맡겨 이동하는 속도를 *표류 속도($v_d$)*라고 정의합니다. 전류 밀도에 적혀있는 속도가 바로 표류 속도입니다.
전류 밀도는 다음과 같이도 표현할 수 있습니다.
$$ J = \sigma E $$
물질에 흐르는 전류 밀도는, 물질에 걸어준 전기장의 세기에 비례한다는 의미이고, 위의 식에서 $\sigma$는 물질의 고유한 값이며, *전도도(Conductivity)*라고 합니다. 그리고 이 식이 바로 *옴의 법칙*의 원래 모습입니다!
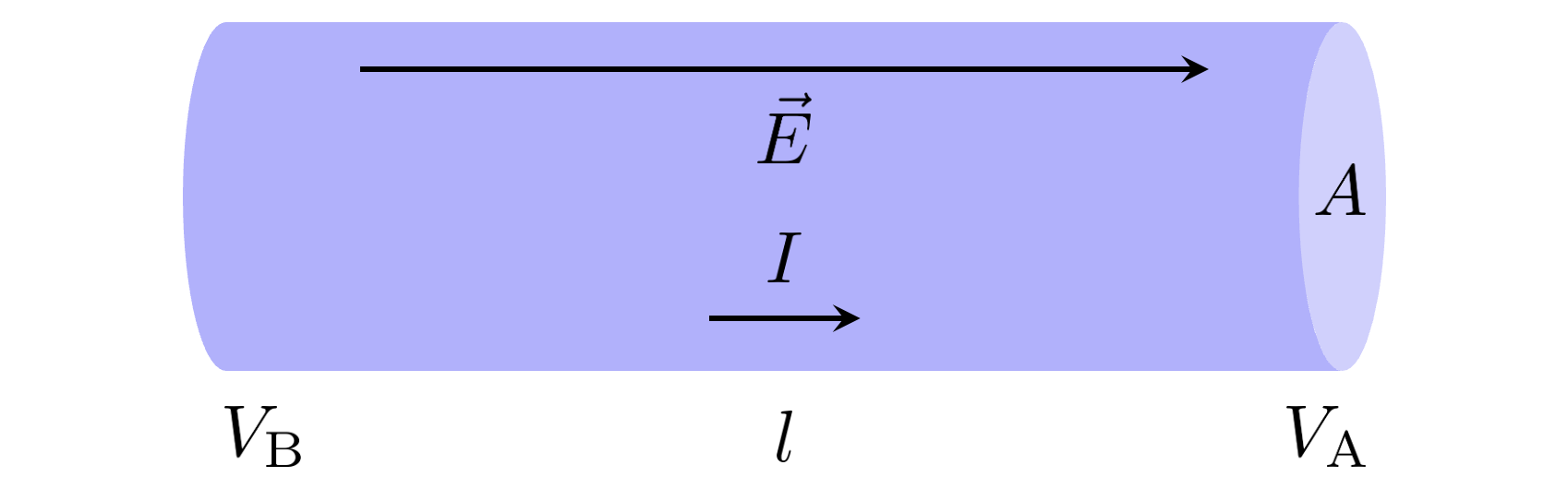
그림과 같이 길이가 $l$인 물질의 양 끝단에 배터리를 연결했고, 전위차(높은 전위 빼기 낮은 전위)가 $\Delta V = V_{\mathrm{B}} - V_{\mathrm{A}}$ 인 상황을 생각해봅시다. 전기장과 전위의 관계에 의해서
$$ \Delta V = E l $$
입니다. 위에서 적어놓은 옴의 법칙을 이용하면 다음 관계식을 얻을 수 있습니다.
$$ \Delta V = \frac{l J}{\sigma} $$
전류 밀도는 $J = I/A$ 이므로,
$$ \Delta V = \left( \frac{l}{\sigma A} \right) I$$
의 관계식을 얻을 수 있습니다. 그런데 여기서 물질의 길이와 단면적, 그리고 물질의 고유한 특성인 전도도 $\sigma$로 정의되어 있는 괄호 안의 항을
$$R = \frac{l}{\sigma A}$$
이라고 정의합니다. 이것이 바로 물질이 가지는 저항의 정의입니다. 따라서 위의 전위차 관계식은 $V = IR$로 정리됩니다. 이것이 우리가 잘 아는 옴의 법칙의 모습입니다.
마치 말장난 같지만, 전도도의 역수를 또다시 *비저항*($\rho$)이라는 물리량으로 정의합니다.
$$\rho = \frac{1}{\sigma}$$
따라서
$$R = \rho \frac{l}{A} $$
이렇게 쓸수도 있습니다. 전도도라는 물리량은 물질 고유의 특성이므로 비저항 역시 물질 고유의 특징입니다.
어떤 물질의 밀도는, 그 물질이 얼마나 큰 부피를 가지건 항상 일정한 그 *물질 고유의 물리량*입니다. 그런데 그 물질의 질량은, 부피가 크거나 작을 때 달라지는, 즉 모양에 따라 바뀌는 *물체의 물리량*입니다. 이것과 마찬가지로,
물질의 비저항은 물질의 모양에 관계없는 물질 고유의 물리량이고, 물질의 저항은 물체의 길이와 단면적 등 모양에 관계있는 *물체의 물리량*입니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 전기 전도의 모형(모델) (0) | 2023.05.06 |
|---|---|
| 동축 케이블의 반지름 방향 저항 (0) | 2023.01.14 |
| 전류의 정의와 개념 (0) | 2022.10.15 |
| 전기장 속의 전기 쌍극자 (0) | 2022.10.10 |
| 축전기의 중앙에 금속이 삽입된 경우 (0) | 2022.10.10 |





