설군의연구소
축전기의 직렬, 병렬 연결 본문
안녕하세요, 설군입니다.

저항이라는 회로의 요소를 직렬 연결, 병렬 연결 하는 것처럼 축전기도 회로의 요소가 될 수 있으므로 직렬 연결, 병렬 연결을 생각해볼 수 있습니다.
* 축전기의 직렬 연결
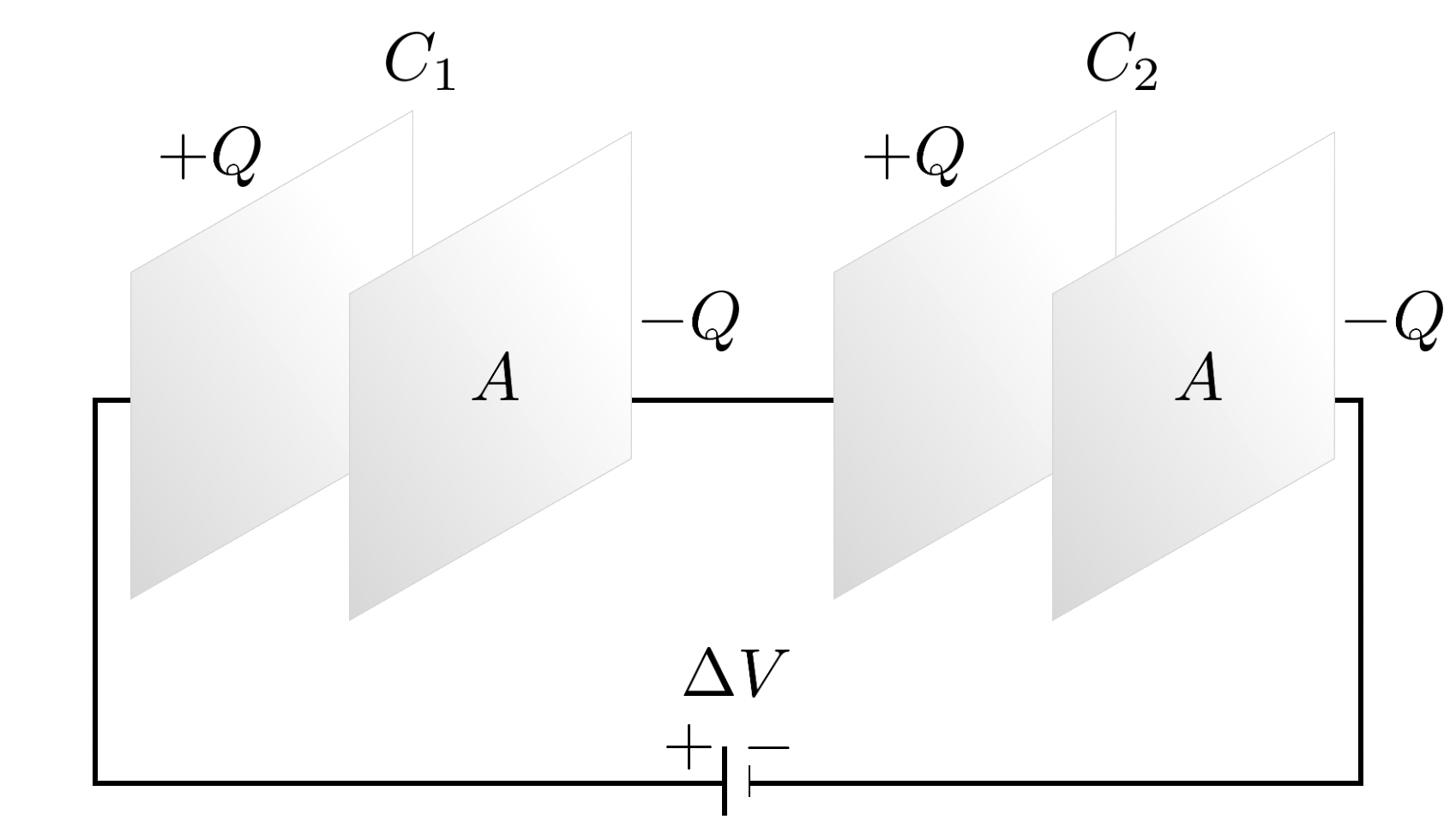
예를 들어 우리가 평행판 축전기가 두 개 있는데, 둘의 전기 용량이 각각 $C_1, C_2$라고 합시다. 위와 같이 연결된 상황이라면 이를 간단하게 회로 그림으로 다음과 같이 나타낼 수 있습니다.

막대기 두 개를 공간을 두고 그려놓은 게 축전기를 의미합니다. 꼭 평행판 축전기가 아니라도, 원통형 축전기나 여러 축전기들을 이런 표식으로 표현합니다.
위와같이 연결된 상황을 축전기의 직렬 연결이라고 합니다. 이런 경우에

두 축전기를, 전기 용량이 $C'$인 한 개의 축전기로 생각할 수 있는데, 이렇게 계산합니다.
$C_1, C_2$의 축전기가 만약 평행판 축전기라고 하고, 둘의 전기 용량이 같다고 생각해봅시다. 두 축전기 극판의 면적이 $A$로 같고, 축전기 각각의 두 극판 사이 떨어진 거리가 $d$로 같다면, 전기 용량은 다음과 같이 써집니다.
$$ C = \varepsilon_0 \frac{a}{d} $$
극판의 면적이 넓을 수록 전기 용량이 커질 것이고, 극판 사이 거리가 가까울 수록 전기 용량이 커진다는 걸 기억하세요!
그런데, 그림에서 보듯이 마치 두 축전기 $C_1, C_2$를 직렬 연결한 것은, 극판 사이 거리가 멀어진 것과 같은 효과가 일어나게 됩니다. 따라서 원래 전기 용량의 식에서, 극판 사이 거리가 $d\rightarrow 2d$가 된 것처럼 계산해주면 됩니다! 따라서
$$ C' = \varepsilon_0 \frac{a}{2d} $$
가 됩니다. 즉 전기 용량이 원래 것보다 절반이 된 것이죠.
이런 식으로 축전기의 직렬 연결에서는, 직렬 연결 할 수록 전기 용량이 작아진다는 걸 기억하세요. 일반적인 식은 다음과 같습니다.
$$ \frac{1}{C'} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots $$
축전기가 여러 개가 직렬 연결 되어있다면, 그 여러 개를 한 뭉텅이로 보았을 때의 전기 용량 $C'$은 위와 같은 관계식으로 구하면 됩니다.
* 축전기의 병렬 연결
반대로 병렬 연결은 다음과 같은 상황입니다.
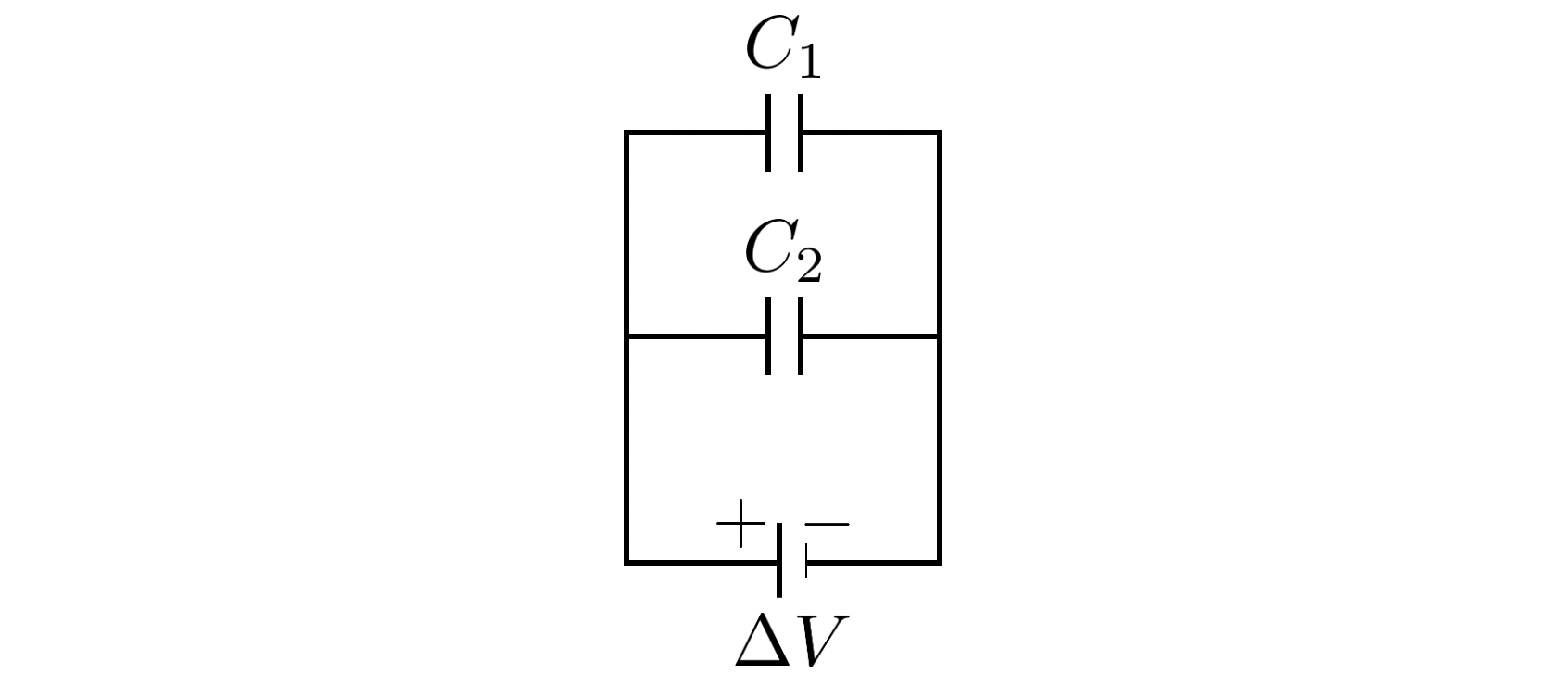
이렇게 연결 된 상황을 축전기의 병렬 연결이라고 합니다.
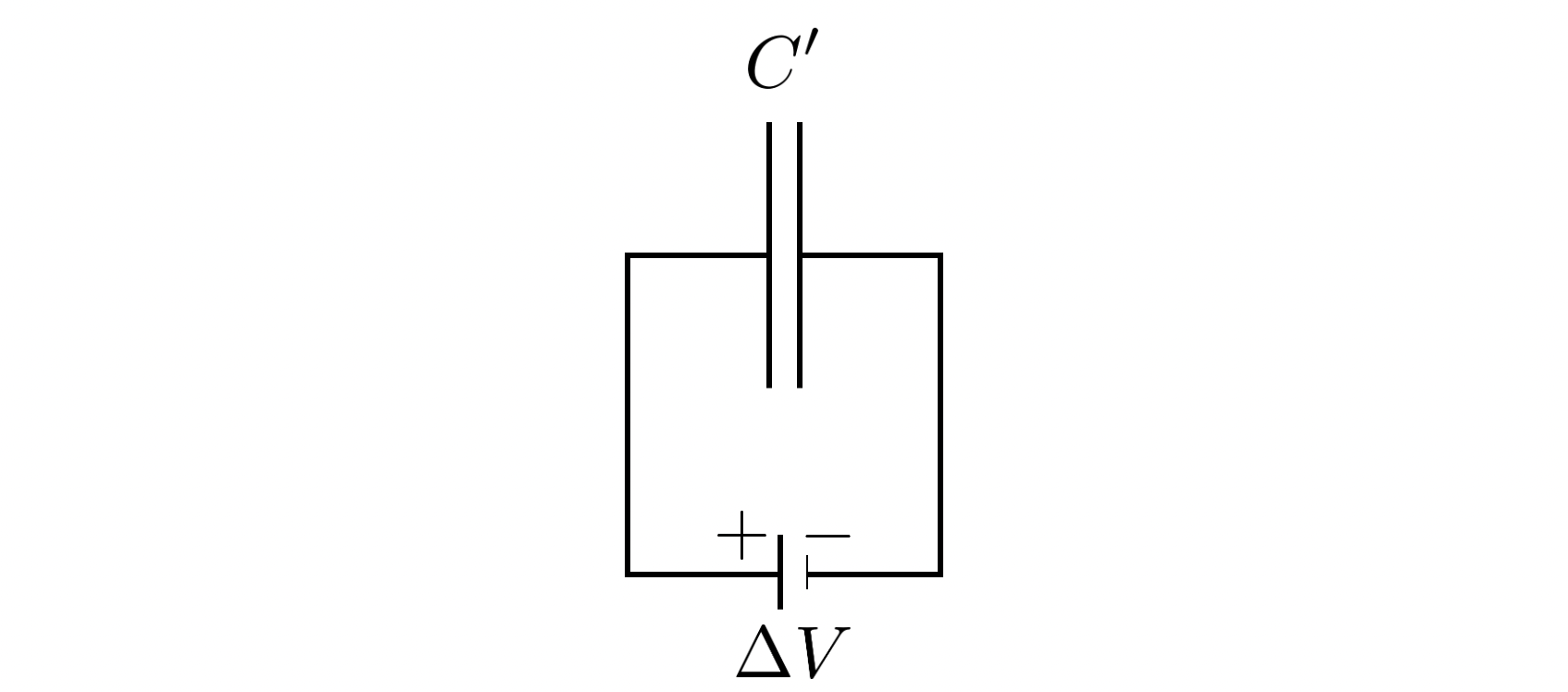
이번에는 마치 축전기 극판 면적이 넓어진 것 같은 효과로 생각하면 됩니다. 두 축전기를 병렬 연결 하면 전기 용량이 커집니다. 따라서
$$ C' = \varepsilon_0 \frac{2A}{d} $$
의 효과가 됩니다. 일반적인 식은
$$ C' = C_1 + C_2 + \cdots $$
입니다.
* 예제
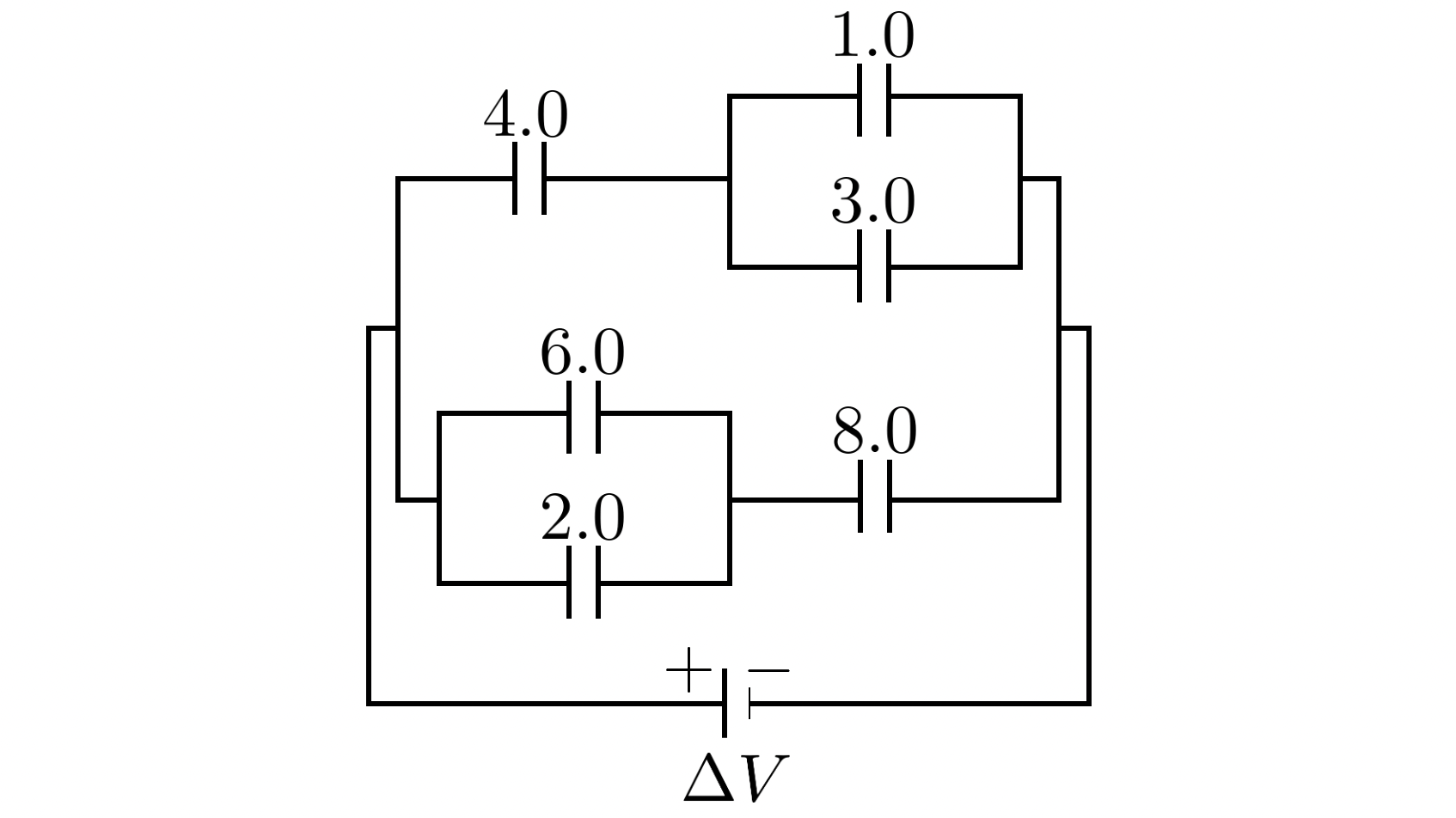
위의 그림과 같이 전기 용량이 패럿 단위로 주어져 있는 회로가 있습니다.
이렇게 축전기가 많이 연결된 회로를 축약해서, 이 회로를 대표하는 하나의 전기 용량 값 $C'$을 찾아봅시다.
하나씩 차근차근 해 나가면 됩니다.
먼저 병렬 연결 된 축전기를 정리해봅시다.
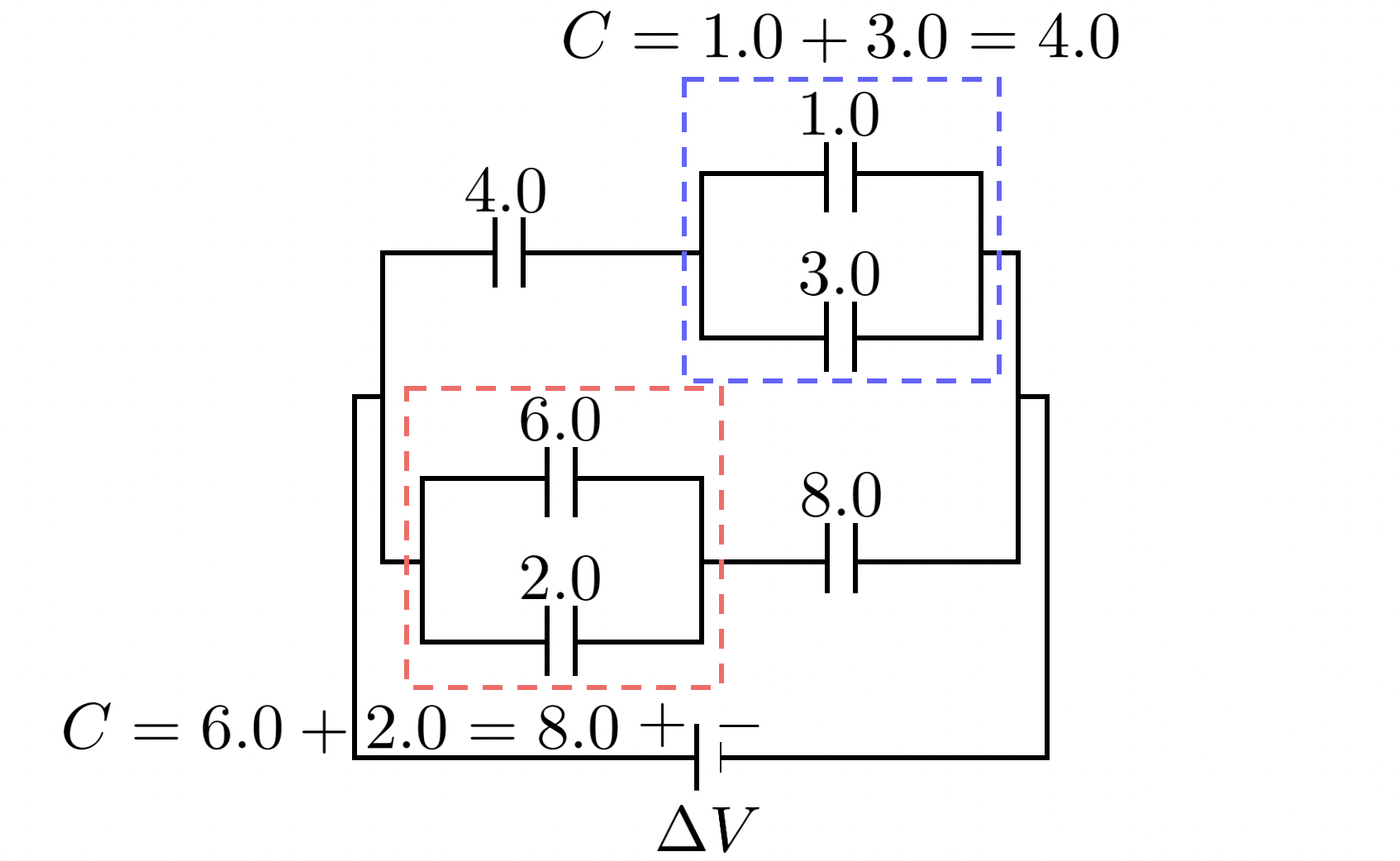
축전기가 병렬 연결 된 경우는 전기 용량이 커지는 상황이므로 간단하게 더해 주면 됩니다.
축약된 모습은 다음과 같습니다.

그럼 이제 4.0, 4.0 짜리가 직렬로 연결된 거랑, 8.0, 8.0 짜리가 직렬로 연결된 걸 계산해봅시다.
이번에는 다음과 같이 계산됩니다.

축전기가 직렬로 연결될 때에는, 전기 용량이 작아진다고 생각하면 됩니다. 4.0짜리 두 개가 직렬 연결 된 경우의 합 전기 용량은 2.0이 되고
8.0짜리 두 개가 직렬 연결 된 경우의 합 전기 용량은 4.0이 됩니다.
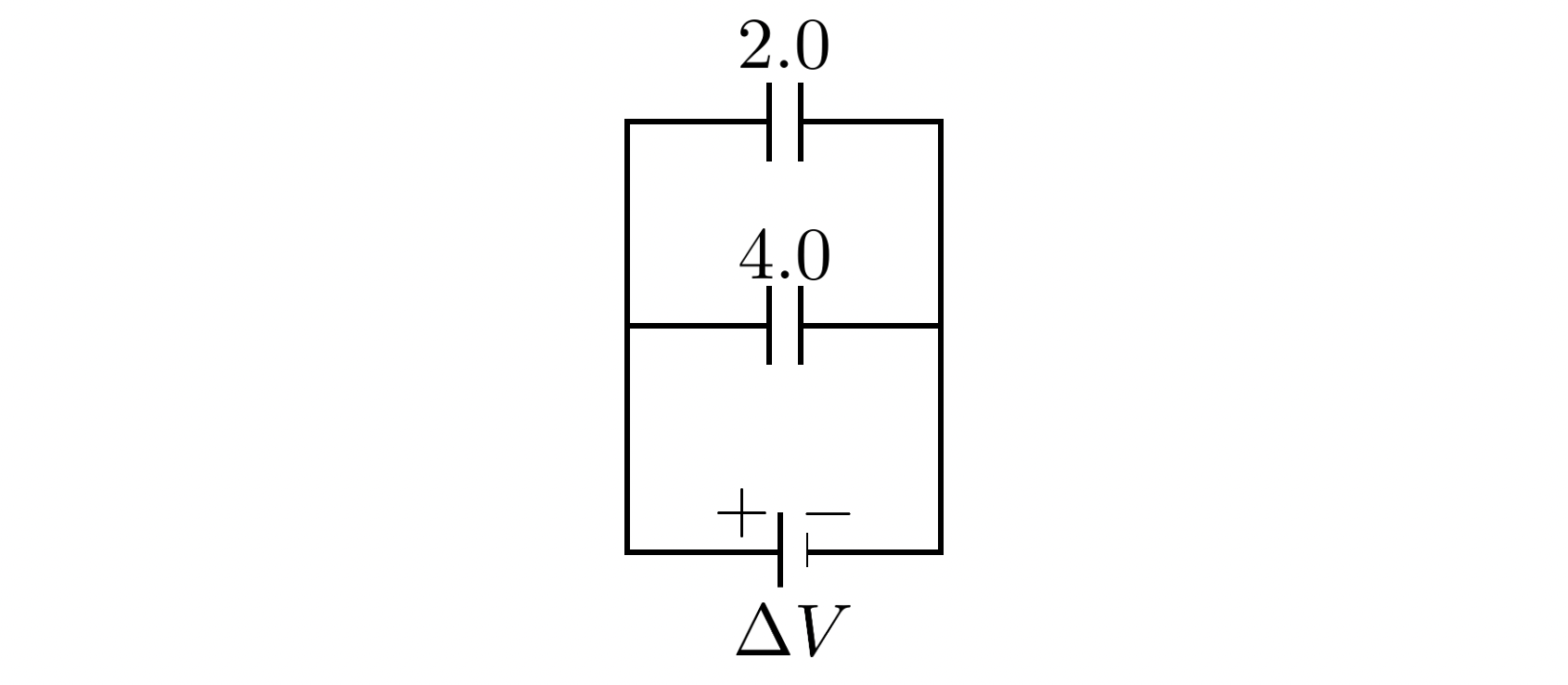
최종적으로는 이렇게 정리됩니다. 마지막으로 이것들은 병렬 연결이므로, 간단하게 $$ C' = 2.0 + 4.0 = 6.0 $$임을 알 수 있지요.
따라서

이 복잡한 회로는

이 회로와 동등합니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 유전체가 포함된 축전기 (1) | 2022.10.10 |
|---|---|
| 축전기에 저장된 에너지 (0) | 2022.10.08 |
| 구형 축전기의 전기 용량 계산 (0) | 2022.10.03 |
| 원통형 축전기의 전기 용량(정전 용량) 계산 (0) | 2022.10.01 |
| 공동(Cavity)을 가지고 있는 도체 (0) | 2022.09.24 |





