설군의연구소
빗면에서의 중력 분해 본문
안녕하세요, 설군입니다.
물체가 어디에 놓여있더라도, 그 물체는 중력을 받습니다. 그런데 빗면에 있을 경우에는 중력을 분해하여 생각해야될 때가 있습니다.
빗면이 물체를 떠받치는 힘과, 지구가 물체를 당기는 힘을 더한 결과가 바로
물체가 빗면으로 가속하면서 내려오는 방향의 힘입니다.

위의 그림과 같이 각도가 $\theta$ 인 빗면에 질량이 $m$ 인 물체가 놓여 있는 상황에서, 물체가 받는 중력을 화살표로 표시하면 위와 같습니다.
그리고, 이 중력은, 어떤 직교 좌표계에서 두 개의 화살표의 합으로 분해할 수 있습니다.
문제를 풀때 가장 편한 건, 물체가 가속운동하는 방향으로 하나의 축을 잡고, 그리고 그것에 수직인 방향으로 나머지 축을 잡는 직교 좌표계를 설정하고 나서.
그리고 그 좌표계와 평행한 두 화살표로 중력을 분해하는 방법입니다.
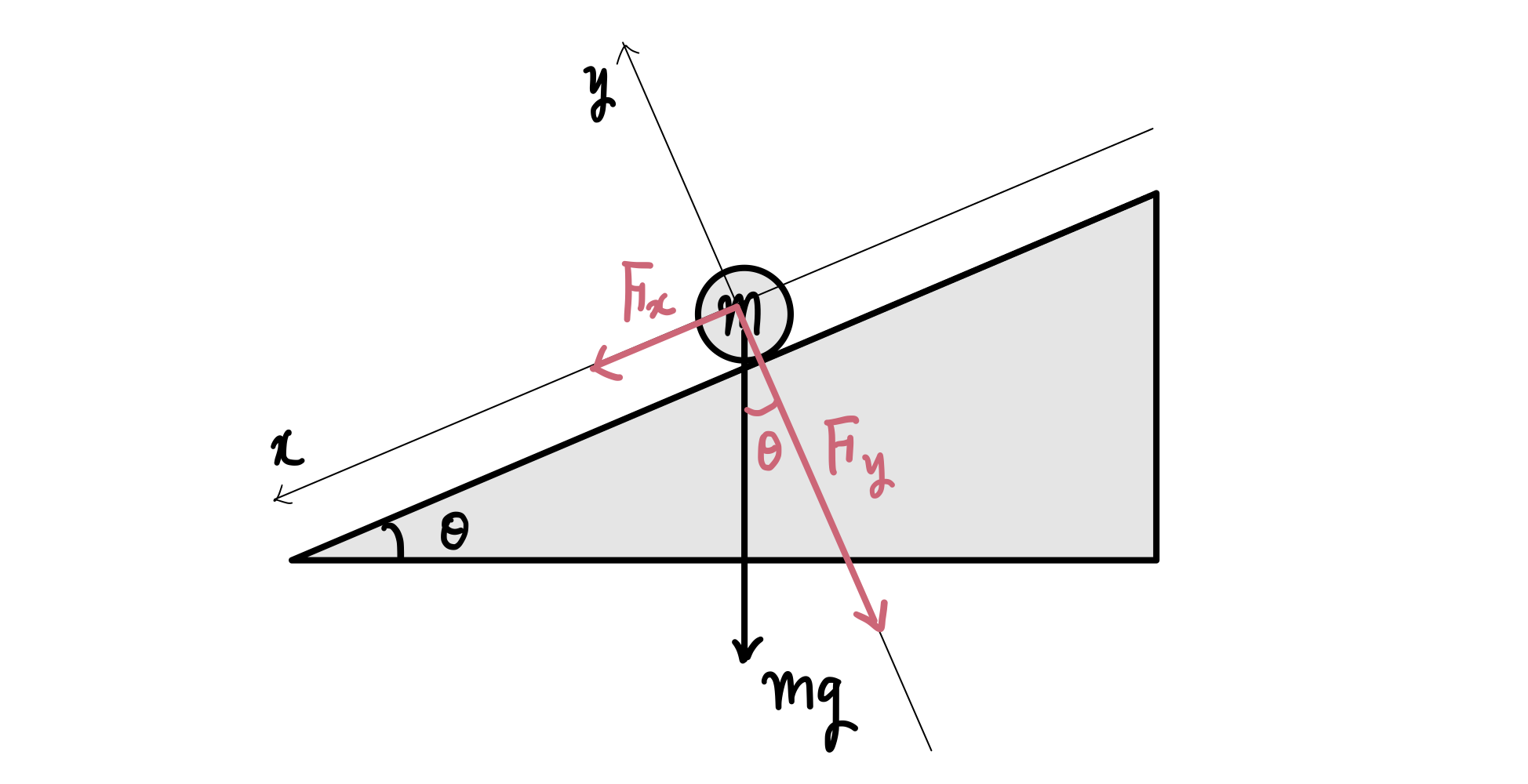
물체가 빗면 아래 방향으로 미끄러지는 상황이라고 생각하고, 그 방향을 $x$ 축으로 하는 직교축을 하나 잡았습니다. 그리고 그것에 대해 수직인 $y$ 축을 하나 잡았습니다.
그러면, 위의 그림과 같이 중력 $mg$ 는 (검정색 화살표) 두 빨간 화살표의 합으로 생각할 수 있습니다. 이 때 두 빨간 화살표는 각각 크기가 $F_x$, $F_y$ 인 벡터 입니다. 각각 $x$, $y$ 축을 향하고 있습니다.
이 결과를 중력을 분해한 것이라고 말합니다.
그렇다면 $F_x$, $F_y$ 라는 힘의 크기는 과연 $mg$, 그리고 $\theta$ 와 무슨 관계가 있을까요?
위의 그림에서 보이는 직각 삼각형을 그리고 나서, 삼각비를 이용하여 삼각형의 변의 길이를 표현해주면 됩니다.

사인과 코사인의 정의를 이용하면, 삼각형의 변의 길이로 표현할 수 있죠
그럼 간단하게 분모를 이항해주면,
$$ F_x = mg \cdot \cos (\theta) $$
$$ F_y = mg \cdot \cos (\theta) $$
로 정리가 됩니다.
우리가 아까 잡은 직교 좌표계를 기준으로, 중력만 놓고 보면, 물체는 직교 좌표계의 $x$ 방향으로 가속 운동을 할 테고,
그리고 직교 좌표계의 $-y$ 방향으로도 가속 운동을 할 것입니다. 왜냐하면 중력의 $-y$ 방향 성분이 있으니까요.
그러나, 실제로는 빗면을 뚫고 물체가 가속운동 하지 않습니다. 빗면이 물체를 떠받쳐주는 힘이 또 있기 때문이지요.
빗면이 물체를 떠받쳐주는 힘의 크기가, $F_y$ 라는 힘의 크기가 서로 같아야만이 물체가 $y$ 방향으로는 알짜힘의 평형을 이루고, 오로지 $x$ 방향으로만 알짜힘을 받을 수 있게 됩니다. 따라서 빗면이 물체를 떠받쳐주는 힘의 크기는 앞서 구한 $F_y$ 와 크기가 같습니다. 이를 수직항력 기호 $N$ 으로 표현하면, 수직항력의 크기는
$$ N = F_y = mg \cdot \cos (\theta) $$
로 정리할 수 있습니다.
'물리학 > 고등물리학' 카테고리의 다른 글
| 볼링공이 30 N의 힘을 가지고 굴러간다? (0) | 2020.03.10 |
|---|---|
| 물리 1에서 위치, 속도, 가속도 - 시간 그래프를 분석하는 방법 (0) | 2020.03.10 |
| 상대성 이론과 상대 속도 (0) | 2020.03.10 |
| 2017 수능특강 물리 1 36쪽 8번 도르래 문제 (0) | 2020.03.10 |
| 움직 도르래 가속 운동 분석 (0) | 2020.03.10 |






