물리학에서 두 벡터의 내적 예제

반응형

안녕하세요, 설군입니다.

 

벡터의 내적에 대한 예제 문제들을 풀어봅시다.

예제 1

주어진 $\vec{A}$ 는 크기가 $5.00$ 단위이고, $\vec{B}$ 는 크기가 $9.00$ 단위입니다. 이 때 두 벡터가 이루는 각도가 $50.0°$ 일 때 두 벡터의 내적 $\vec{A} \cdot \vec{B}$ 을 구해봅시다.

 

벡터 $\vec{A}$ 의 $x$ 성분의 크기와 $y$ 성분의 크기를 각각 $A_x$, $A_y$ 라고 표현할 수 있습니다.

마찬가지로 벡터 $\vec{B}$ 에 대해서도 이 벡터의 성분의 크기를 각각 $B_x$, $B_y$ 라고 표현할 수 있습니다.

이 때 두 벡터를 위의 표현으로 다시 적어보면,

$$ \vec{A} = A_x \hat{x} + A_y \hat{y} $$

$$ \vec{B} = B_x \hat{x} + B_y \hat{y} $$

이렇게 적을 수 있습니다.

 

문제에 주어진 대로, 두 벡터의 크기가 만족해야 하는 식은 다음과 같습니다.

$$ | \vec{A} | = \sqrt{ (A_x)^2 + (A_y)^2} = 5.00 $$

$$ | \vec{B} | = \sqrt{ (B_x)^2 + (B_y)^2} = 9.00 $$

이 관계를 기억해놓고, 이제 내적에 대한 식을 적어봅시다.

 

$$ \vec{A} \cdot \vec{B} = | \vec{A} | \cdot |\vec{B} |  \cdot \cos (\theta) $$

 

여기에 벡터들의 크기와, 두 벡터가 이루는 각도를 대입해주면,

 

$$ = |5.00| \cdot |9.00| \cdot \cos (50.0°) = 28.9 $$

 

입니다. 두 벡터의 내적의 결과는 숫자 값으로 결과가 나와야 합니다.

 

예제 2

다음 그림과 같이 힘 벡터와 변위 벡터가 주어졌을 때, 두 벡터의 내적 값을 구해봅시다.

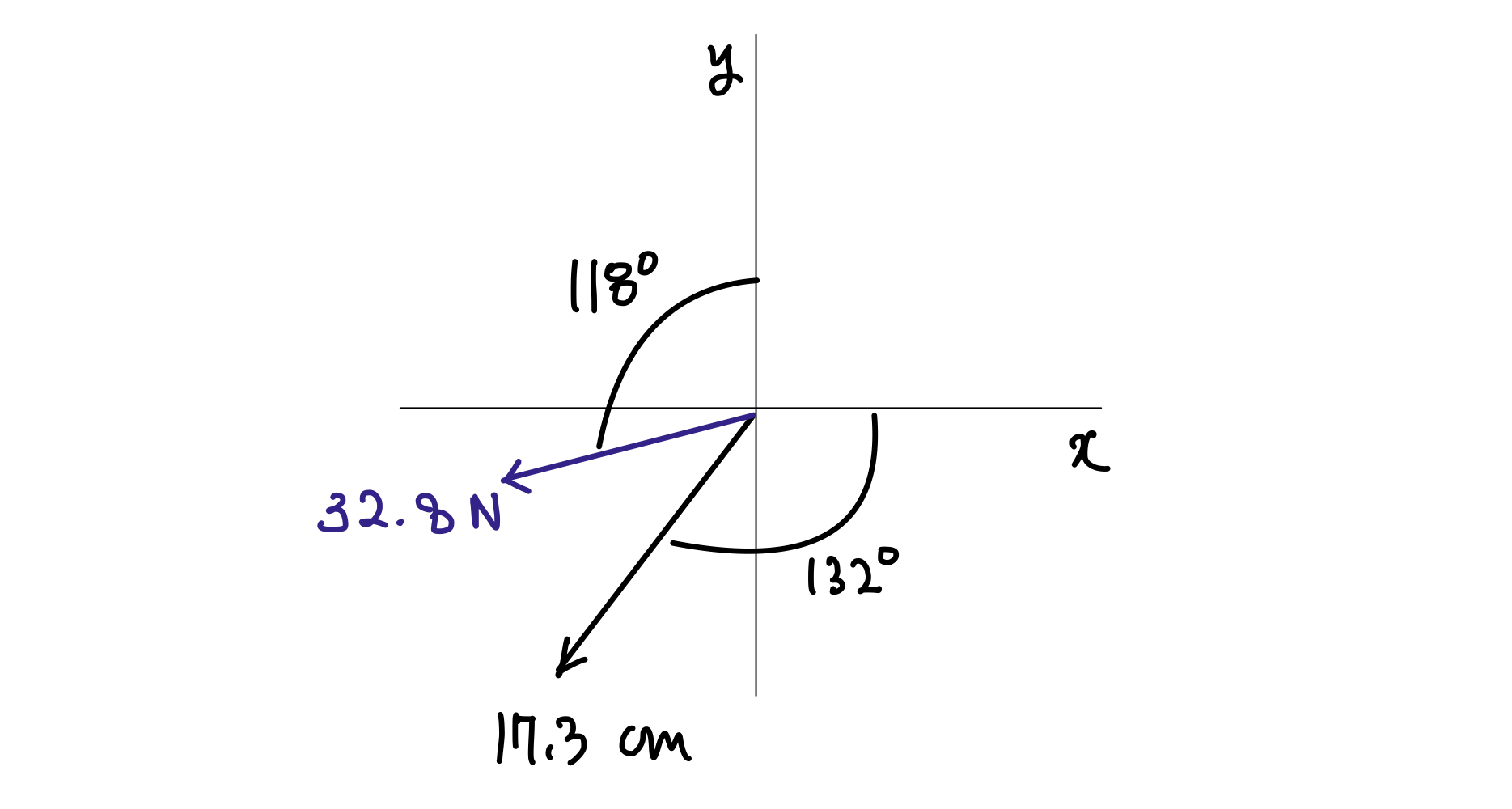
두 벡터의 내적 기본 공식을 다시 생각해봅시다.

$$ \vec{A} \cdot \vec{B} = | \vec{A} | \cdot | \vec{B} | \cdot \cos (\theta) $$

두 벡터를 내적할 때에는, 두 벡터의 크기를 곱하고, 그리고 두 벡터가 이루는 각도의 코사인 값을 곱해주는 것입니다.

벡터의 크기는 각각 문제에 주어져 있습니다.

그러므로 각도만 구하면 되는데, 그림에 주어진 각도를 이용해서 두 벡터가 이루는 각도를 구해봅시다.

1사분면의 각도가 $90°$ 이므로, 두 벡터가 이루는 각도 $\theta$ 는 다음 식을 만족해야 합니다.

$$ 118° + 90° + 132° + \theta = 360° $$

따라서

$$ \theta = 20° $$

입니다.

그러므로 내적값은,

$$ \vec{A} \cdot \vec{B} = | 32.8 | \cdot |17.3 | \cdot \cos (20°) = 533 \  \rm{N} \cdot \rm{cm} $$

가 됩니다. 단위도 잘 적어주어야 합니다.

 

예제 3

내적의 정의를 이용해서, 두 벡터 사이의 각도를 구해봅시다.

(a) $\vec{A} = 3 \hat{x} - 2 \hat{y}$ 와 $\vec{B} = 4 \hat{x} - 4 \hat{y} $ 사이의 각도

내적 식을 다시 생각해봅시다.

$$ \vec{A} \cdot \vec{B} = | \vec{A} | \cdot | \vec{B} | \cdot \cos (\theta) $$

이 내적은 다음과 같이 벡터의 성분별로도 쓸 수 있습니다.

$$ \vec{A} \cdot \vec{B} = A_x \cdot B_x + A_y \cdot B_y $$

문제에서 주어진 두 벡터는 각각 성분을 알려줬으므로 우리는 이 값을 계산할 수 있습니다!

$$ \vec{A} \cdot \vec{B} = 3 \cdot 4 + (-2) \cdot (-4) = 12 + 8 = 20 $$

입니다.

그런데, 이 계산된 결과를 원래의 내적 식이랑 함께 적어봅시다.

$$ 20 = | \vec{A} | \cdot | \vec{B} | \cdot \cos (\theta) $$

이렇게 적을 수 있는데요, 여기서도 우리가 값을 알고있는 게 있습니다. 바로 두 벡터의 각각의 크기들입니다.

그걸 다시 적어주면

$$ 20 = \sqrt{3^2 + (-2)^2} \cdot \sqrt{4^2 + (-4)^2} \cdot \cos (\theta) $$

이렇게 적을 수 있습니다. 계산하여 정리해주면

$$ 20 = \sqrt{13} \cdot \sqrt{32} \cdot \cos (\theta) $$

이므로, 우리는 각도를 구할 수 있게됩니다.

$$ \cos (\theta) = \frac{20}{\sqrt{13} \cdot \sqrt{32}} $$

이므로, 각도는

$$ \theta = \cos ^{-1} \left( \frac{20}{\sqrt{13} \cdot \sqrt{32}} \right) $$

$$ \theta = 27.5° $$

입니다.

 

(b) $\vec{A} = -2 \hat{x} + 4 \hat{y} $ 와 $ \vec{B} = 3 \hat{x} - 4 \hat{y} + 2 \hat{z} $ 사이의 각도

이번에는 두 벡터 중 하나가 삼차원 공간의 벡터입니다.

이 경우에는 벡터 $\vec{A}$ 도 삼차원 공간상의 벡터라고 생각하고, 이 벡터의 $A_z$ 즉 $z$ 방향 성분이 $0$ 이라고 생각하고 문제를 해결하면 됩니다.

$$ \vec{A} \cdot \vec{B} = | \vec{A} | \cdot | \vec{B} | \cdot \cos (\theta) $$

이므로 곧바로 각도에 대한 식으로 변환해주면

$$ \cos (\theta) = \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| \cdot |\vec{B}|}$$

따라서

$$ = \frac{A_x \cdot B_x + A_y \cdot B_y + A_z \cdot B_z}{\sqrt{A_x^2 + A_y^2 + A_z^2} \cdot \sqrt{B_x^2 + B_y^2 + B_z^2}} $$

$$ = \frac{(-2)\cdot 3 + 4 \cdot (-4) + 0 \cdot 2}{\sqrt{20} \cdot \sqrt{29}} $$

가 됩니다. 그러므로 각도는

$$ \theta = 156.1° $$

가 됩니다.

 

(c) $\vec{A} = \hat{x} - 2 \hat{y} + 2 \hat{z}$ 와 $\vec{B} = 3 \hat{y} + 4 \hat{z} $ 사이의 각도

역시 같은 방법으로 곧바로 구해봅시다.

$$ \cos (\theta) = \frac{ \vec{A} \cdot \vec{B}}{|\vec{A}| \cdot |\vec{B}} $$

이므로,

$$ = \frac{1 \cdot 0 + (-2) \cdot 3 + 2 \cdot 4}{\sqrt{1^2 + (-2)^2 + 2^2} \cdot \sqrt{0^2 + 3^2 + 4^2}} $$

$$ \theta =  \cos ^{-1} \left( \frac{2}{15} \right) = 82.34° $$

입니다.