반응형
Notice
Recent Posts
Recent Comments
Link
설군의연구소
등가속도 공식은 어떻게 나왔는가? (물리 1) 본문
반응형
안녕하세요, 설군입니다.
물리학에서 위치, 속도, 가속도-시간 그래프가 주어진 문제를 풀 때에는,
그 그래프의 기울기나 넓이를 이용해서 답을 구합니다.
그런데 우리가 잘 알고있는 등가속도 공식 세 가지는
위치, 속도, 가속도-시간 그래프에서 기울기와 넓이를 구하는 과정에서도 유도할 수 있습니다.
다음은 속도-시간 그래프입니다.

그래프의 기울기는 가속도와 같고, 다음과 같이 구할 수 있습니다.
$$ a = \frac{v-v_0}{t} $$
따라서 위의 식으로부터 다음 식을 이끌어낼 수 있습니다.
$$ v - v_0 = at $$
이제 위의 그래프에서 0초부터 $t$초까지의 넓이를 구하려면, 다음과 같이 색칠된 영역의 넓이를 구하면 되는데,

이 넓이는 삼각형 하나와 사각형 하나의 넓이로 쪼개서 구할 수 있습니다.
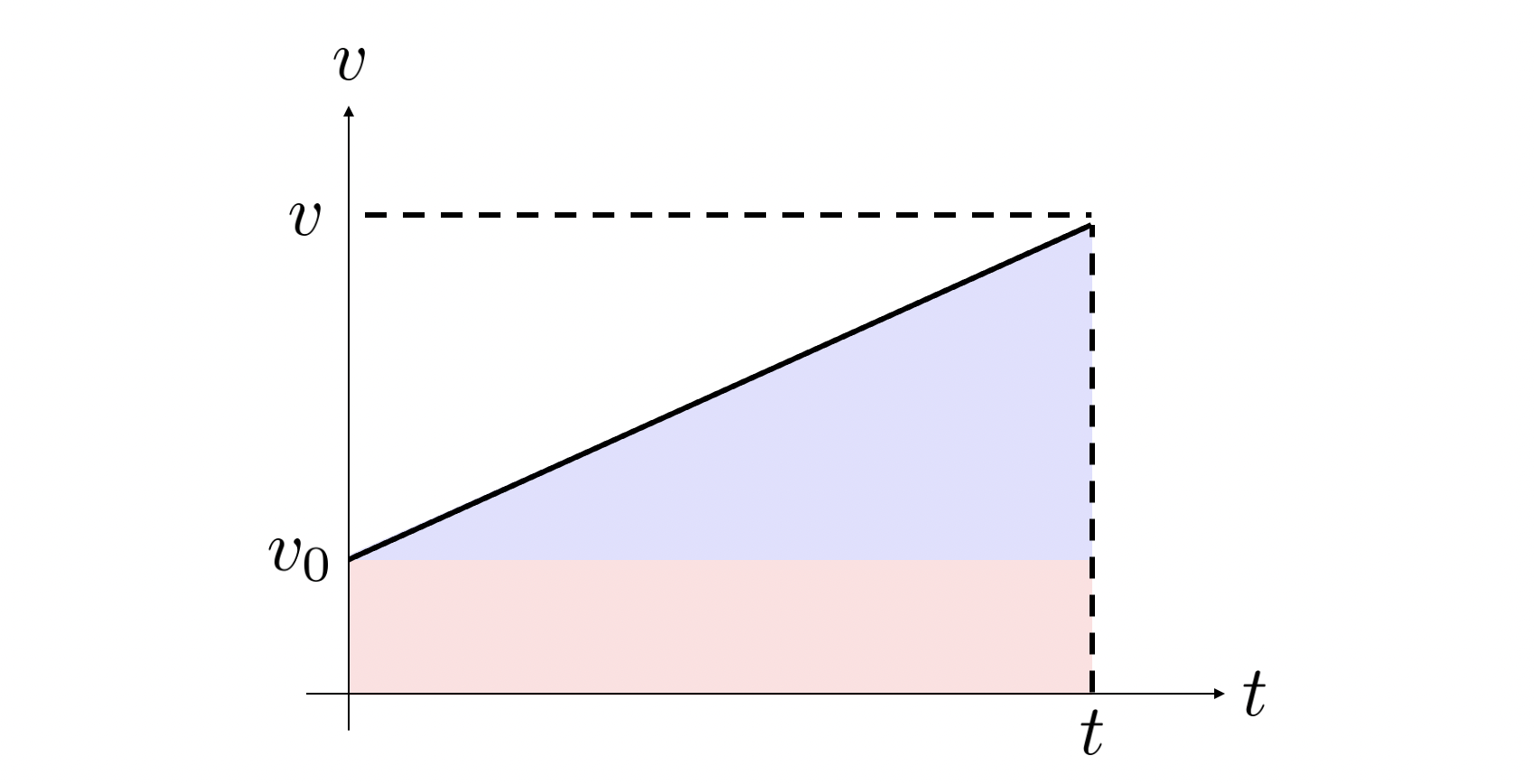
삼각형의 넓이는 $ \frac{1}{2} \cdot t \cdot (v-v_0)$ 이고,
사각형의 넓이는 $t \cdot v_0$ 이므로,
두 넓이를 더한것이 최종 넓이이므로 그것이 바로 이동거리입니다. 따라서 이동거리는
$$ s = \frac{1}{2} (v-v_0)t + v_0 \cdot t $$
가 되는데, 앞서 기울기를 이용해서 구했던 $ v - v_0 = at$ 식을 대입해주면,
$$ s = v_0 t + \frac{1}{2} at^2 $$
이렇게 잘 아는 등가속도 공식이 등장합니다!
그래프를 더 자세하게 분석하는 방법은 다음 글을 참고해보세요.
https://seolgoons.tistory.com/20
반응형
'물리학 > 고등물리학' 카테고리의 다른 글
| 물리 1, 저음 증폭, 고음 증폭 스피커 문제 해법 (0) | 2020.03.11 |
|---|---|
| 평균 속력과 평균 속도 (0) | 2020.03.10 |
| 도르래 문제 풀이 (0) | 2020.03.10 |
| 물리 1, 물리 2를 할 때 알아두면 좋은 것 4. 벡터의 분해 (0) | 2020.03.10 |
| 물리 1, 물리 2를 할 때 알아두면 좋은 것 3. 벡터의 곱셈 - 내적과 외적 (0) | 2020.03.10 |
Comments




