고리 도선이 자기장 영역을 통과할 때

 

 

반응형

안녕하세요, 설군입니다.

 

 

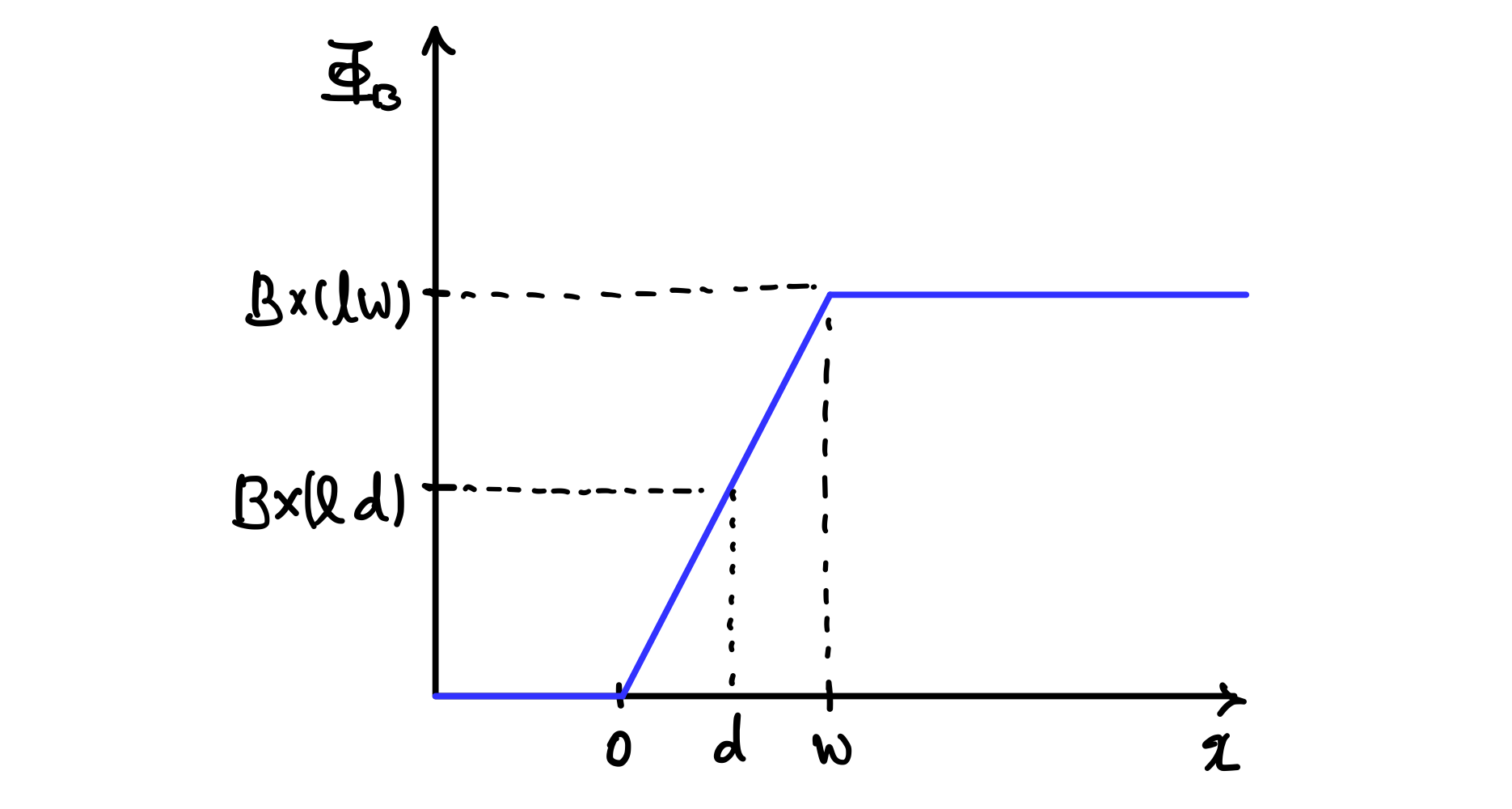
위 그림과 같이 자기장이 화면을 뚫고 들어가는 방향으로 ${\overrightarrow{B}}_{\mathrm{in}}$ 으로 균일하게 펼쳐져 있는 공간이 있습니다. 이 공간의 가로 길이는 총 $3w$ 입니다. 이 공간에, 왼쪽에서 출발해서 오른쪽으로 속도 $\overrightarrow{v}$ 로 일정하게 움직이는 ㅁ 모양의 도선이 있습니다. 이 고리 도선의 세로 길이는 $l$, 가로 길이는 $w$ 라고 하겠습니다.

고리 도선의 오른쪽 부분이 자기장 영역에 닿은지점을 그림과 같이 $x=0$ 으로 출발점으로 잡겠습니다. 그리고 $x$ 가 증가함에 따라 고리 도선을 통과하는 자기 플럭스가 어떻게 되는지를 생각해보면 다음과 같습니다. 

자기 플럭스 ${\mathrm{\Phi }}_{\mathrm{B}}$ 라는 물리량은 결국 자기장과 면적의 곱으로 주어지게 됩니다. 물론 자기장이 면을 어떤 각도로 통과하느냐도 중요합니다. 이 문제에서는, 고리 도선을 이루는 면과, 자기장이 수직하기 때문에, 고리 도선에 통과하는 자기 플럭스는 자기장이 닿아있는 부분의 면적 곱하기 자기장의 세기로 계산하면 됩니다.

 

위 그림과 같이 $d$ 만큼 고리 도선이 닿아 있다고 한다면, 이 순간만큼은 고리 도선에 통과하는 자기 플럭스는

$${\mathrm{\Phi }}_{\mathrm{B}}=B\times (d\cdot l)$$

인 것입니다. 그런데 고리 도선이 서서히 오른쪽으로 (일정한 속력으로) 이동한다면, 고리 도선이 자기장 영역에 점점 발을 들이게 됩니다. 이런 과정에서 $d$ 는 거리에 따라 일정하게 증가할것입니다. (속도가 일정하니까)

그러므로 ${\mathrm{\Phi }}_{\mathrm{B}}$ 가 일정하게 증가합니다.

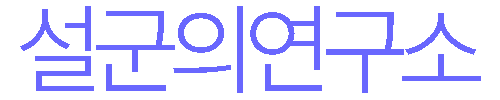
따라서 그래프로 그려보면 고리 도선의 모든부분이 자기장 영역에 들어오기까지는 일차 함수의 형태로 자기 플럭스가 서서히 증가하게 됩니다.

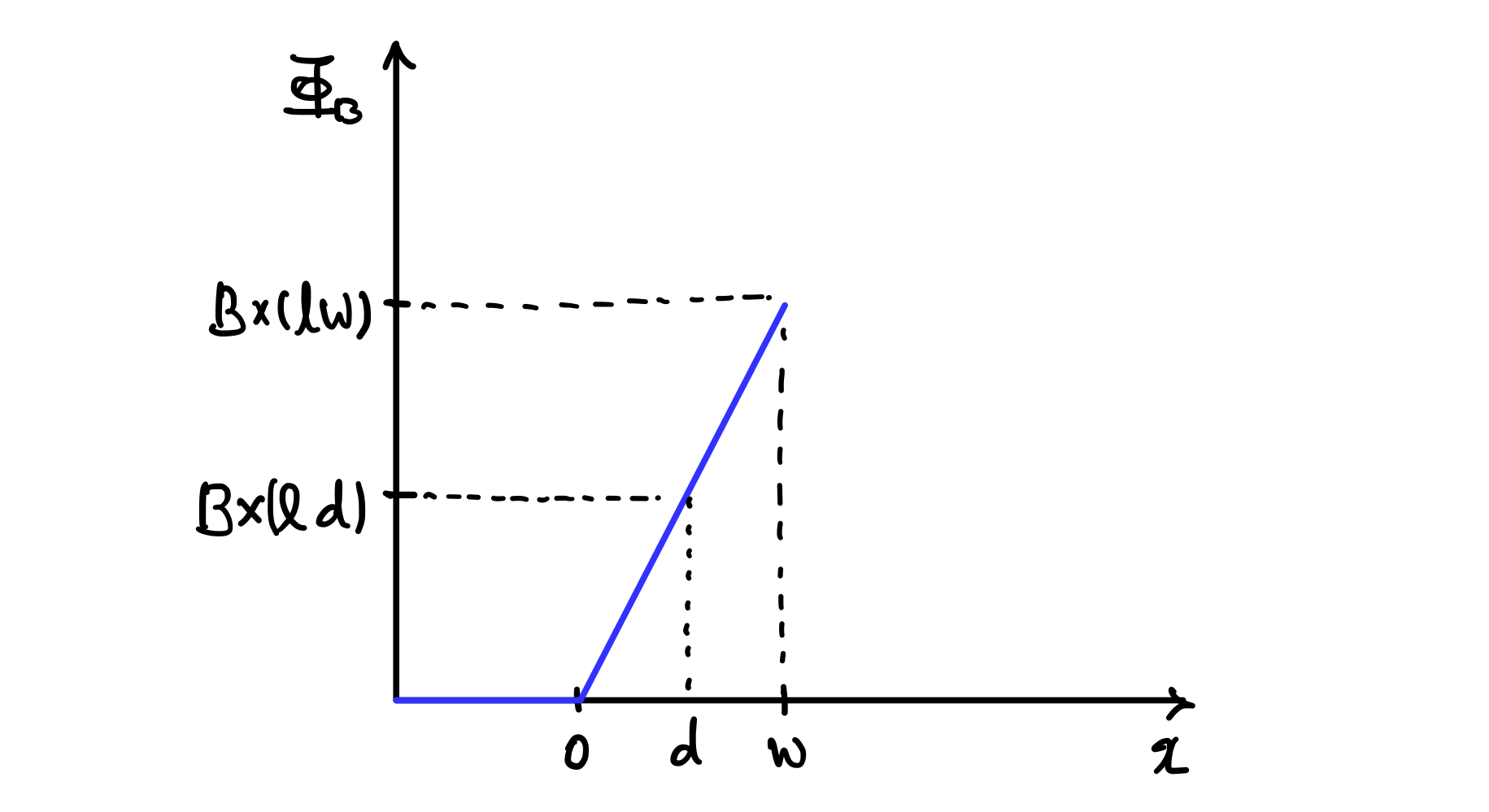
그리고 나서 고리 도선이 완전히 자기장 영역에 들어온 이후에는, 면적을 통과하는 자기장이 일정하므로, 자기 플럭스도 계속 일정합니다.

그리고 나서는, 영역을 빠져나가는 순간부터 중요해지게 됩니다. 자기 플럭스는 다시 감소하게 될 것입니다.

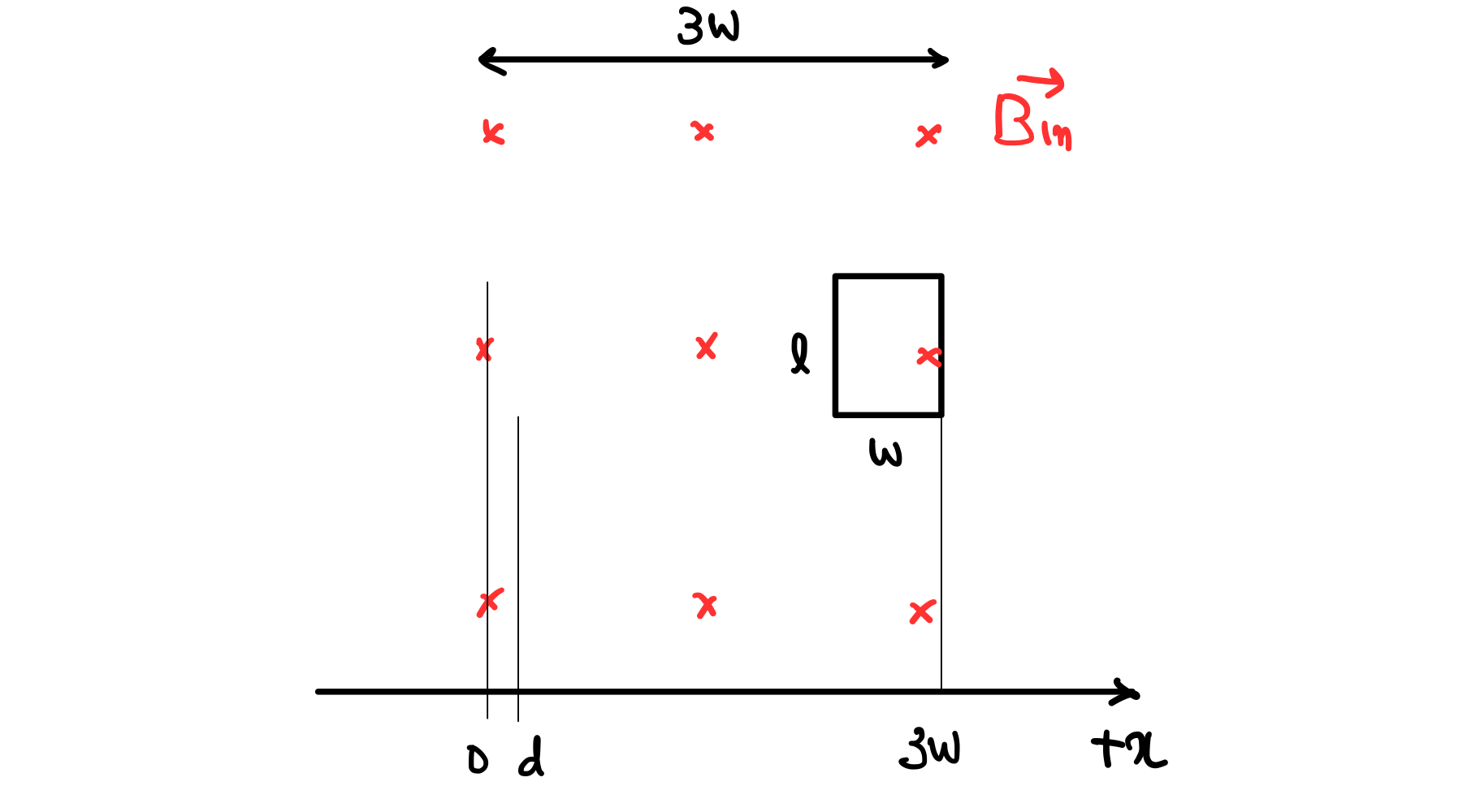
이렇게 고리 도선의 오른쪽 끝이 자기장의 마지막 영역에 걸친 순간, 즉 $x=3w$ 인 순간부터는, 다시 자기장이 선형적으로 감소합니다. 최종적으로 완벽하게 고리 도선의 왼쪽 끝 부분이 자기장 영역에서 빠지는 순간은 $x=4w$ 입니다. 최종적으로 그래프는

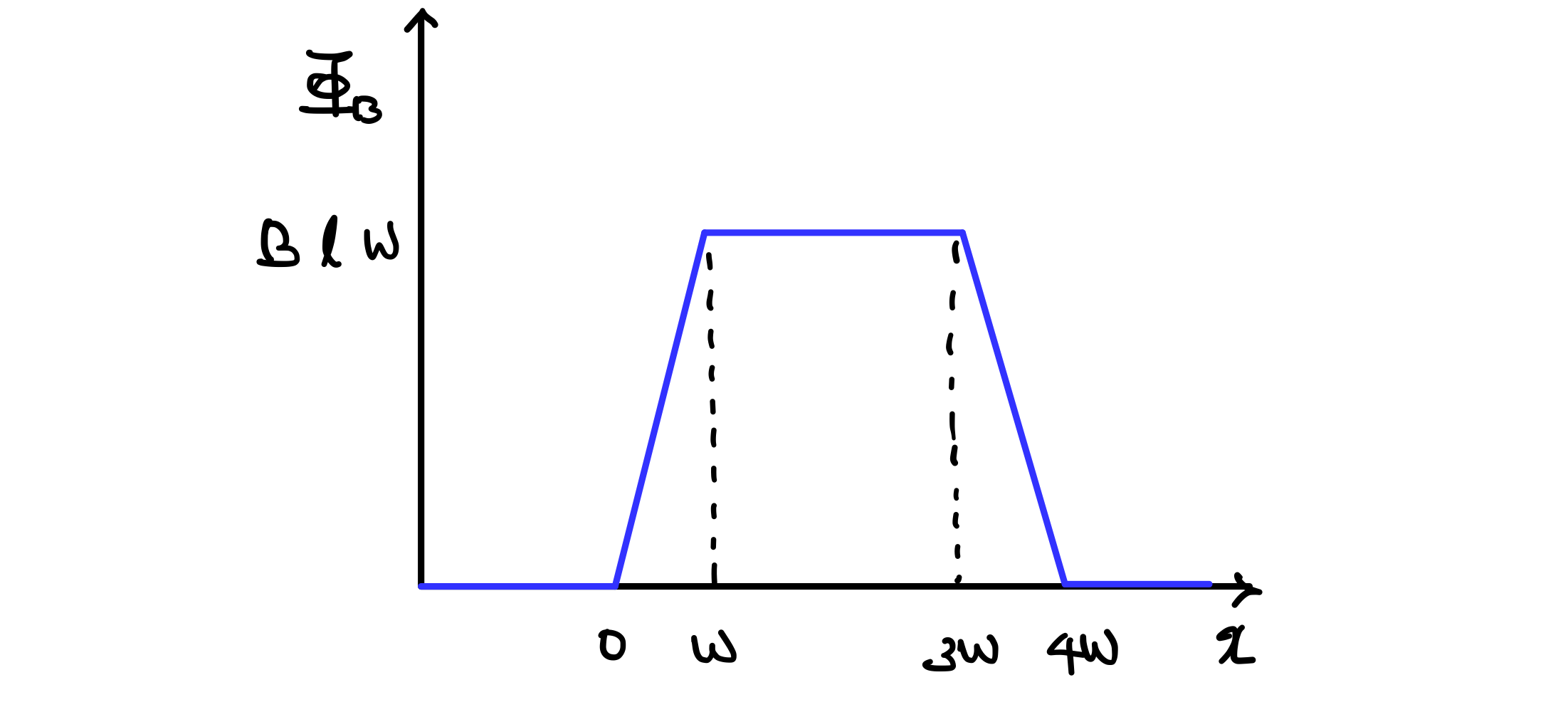
이렇게 그려지게 됩니다. 고리 도선을 통과하는 자기 플럭스가, 화면을 뚫고 들어가는 방향으로 생기긴 생기는데 고리 도선의 위치에 따라서 어떻게 생기는지를 해석해봅시다.

고리 도선이 자기장 영역 밖에 있을 때에는, 고리 도선을 통과하는 자기장이 없으므로 자기 플럭스도 0 입니다.

자기장 영역에 다가가며 발을 걸치는 순간, 고리 도선을 통과하는 자기장이 있으므로 플럭스가 슬슬 생기는데

고리 도선이 점점 더 진행하는 순간, 자기장에 걸친 면적이 넓어지니까 (자기장이 세지는게 아닙니다) 플럭스가 점점 증가합니다.

그러다가 완전히 고리 도선이 영역에 모두 발을 들인 이후에는, 면적도 그대로고 자기장도 그대로이므로 자기 플럭스는 그대로 유지가 됩니다.

그리고 자기장 영역에서 나오면서 자기 플럭스는 줄어듭니다.

---

고리 도선을 통과하는 자기 플럭스가 *변할 때* 고리 도선에는 유도 기전력이 생기면서, 유도 전류가 흐르게 됩니다. 유도 전류가 흐르는 방향은 렌츠의 법칙을 이용해 알 수 있습니다.

고리 도선을 통과하는, 화면을 뚫고 들어가는 방향의 자기 플럭스가 점점 많아지는 상황인 $x=0-x=w$ 구간을 생각해봅시다.

 

이 구간에서 자기 플럭스가 변하고 있기 때문에, 유도 전류가 흐릅니다. 유도 전류가 흐르는 방향은 오른손을 이용하여 쉽게 알 수 있습니다.

고리 도선 입장에서, 화면을 뚫고 들어가는 방향의 자기 플럭스가 점점 많아지므로, 이를 막아내기 위한 플럭스를 만들기 위해 오른손 엄지 손가락을 향하면 됩니다.

막아내려면 화면을 뚫고 나오는 방향으로 엄지 손가락을 향해야 합니다. 그렇게 하고 난 뒤, 오른손 네 손가락이 향하는 방향이 유도 전류의 방향입니다. 즉 반시계 방향의 유도 전류가 흐르게 됩니다!

 

고리 도선을 통과하는 자기 플럭스가 변할 때 유도 전류가 흐르는데, 그 유도 전류는 유도 기전력과 도선의 저항 값으로 정해집니다.

$$V=IR$$

로 정해지듯이, 여기서 전압은 유도 기전력에 해당하고, 전류는 유도 기전력에 의해 생기는 유도 전류, 그리고 저항은 도선의 저항을 의미합니다. 따라서

$$\epsilon =IR$$

로 적을 수 있습니다. (단순히 전압 $V$ 를 유도 기전력의 표현 문자인 $\epsilon$ 으로 바꾼 것입니다.)

 

그 유도 기전력의 크기는

$$\epsilon =-\frac{d{\mathrm{\Phi }}_{\mathrm{B}}}{dt}$$

입니다. 고리 도선을 통과하는 자기 플럭스가 시간에 따라 얼마만큼 변하느냐가 유도 기전력을 의미합니다. 또한, 이건 미분이므로, $y$ 축이 자기 플럭스이고 $x$ 축이 시간인 그래프에서, 그래프의 기울기를 의미합니다. 우리가 위에서 그린 그래프는, 비록 $x$ 축이 거리에 대한 그래프이긴 하지만, 이 상황에서 고리 도선은 일정한 속력으로 움직이고 있습니다. 그러므로 일정한 시간동안 일정한 거리만큼 이동하므로, $x$ 축도 시간에 비례한다고 생각하면 되므로, 기울기를 구해볼 수 있습니다.

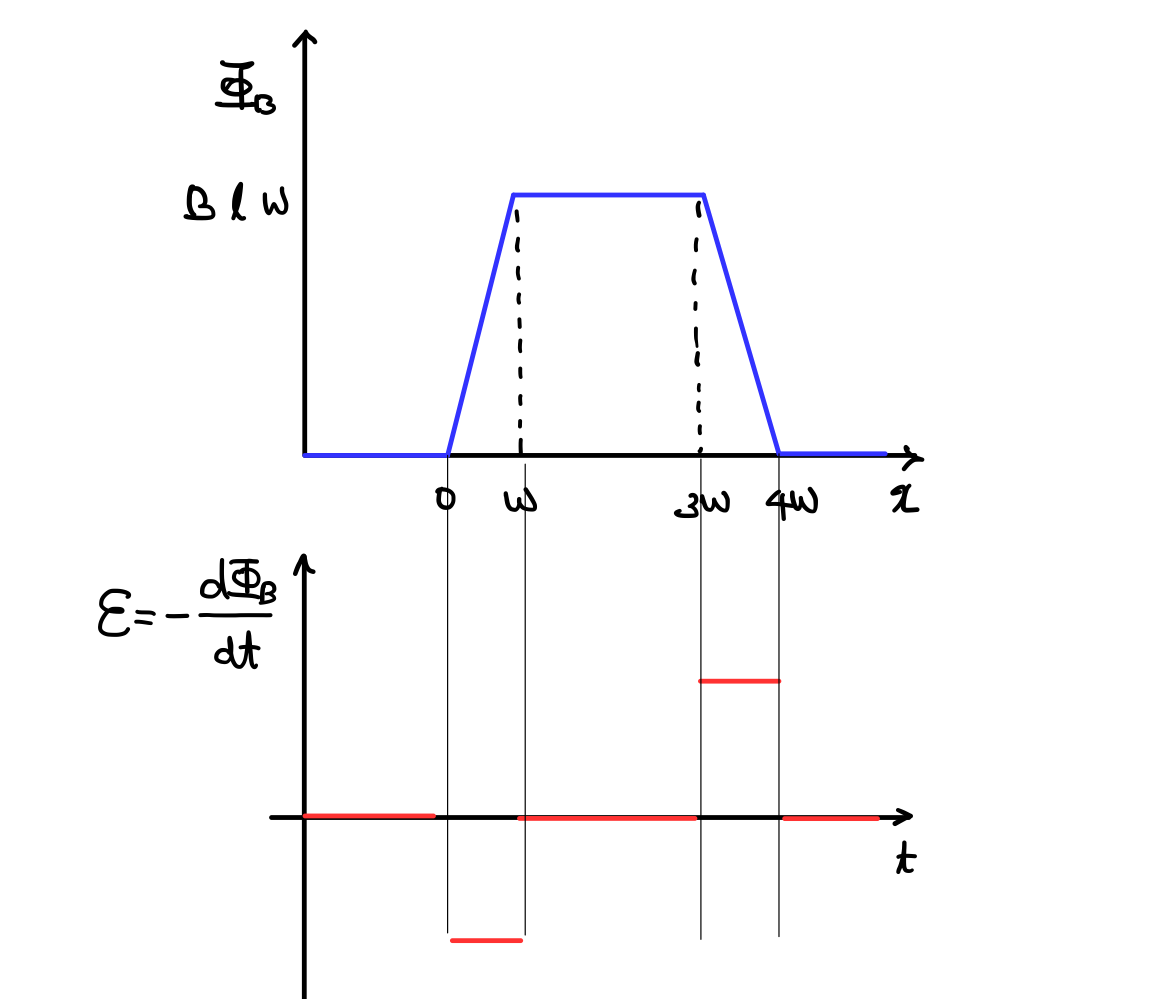
그래프와 비교해서 그려보면 이렇습니다. 파란색 그래프에서의 각각 구간에서 기울기를 구한 후 마이너스 부호를 붙여 빨간 그래프로 옮긴 것입니다.

$0-w$ 구간은 파란 그래프의 기울기가 양수 이므로, 마이너스 부호를 붙이면 음수인 임의의 값이 되므로 빨간 그래프 상에서 음수 위치에 직선을 그리고

$w-3w$ 구간은 파란 그래프의 기울기가 0이므로, 빨간 그래프 상에서도 0으로 표시해주고,

$3w-4w$ 구간은 파란 그래프의 기울기가 음수 이므로, 마이너스 부호를 다시 붙이면 양수인 임의의 값이 되므로, 빨간 그래프 상에서 양수 위치에 직선을 그리면 됩니다.

 

빨간 그래프가 의미하는 것은, 위치(시간)에 따라 고리 도선에 (렌츠의 법칙에 따라서) 생기는 유도 기전력을 말합니다. 유도 기전력의 크기는 빨간 그래프에서의 값들의 절댓값을 생각하면 되고, 유도 기전력의 부호가 의미하는 건, 유도 전류가 흐르는 방향을 의미합니다.

(위의 경우에는, 음수 유도 기전력의 구간에서는 고리 도선에 유도 전류가 반시계 방향으로 흐르고. 양수 유도 기전력의 구간에서는 고리 도선에 유도 전류가 시계 방향으로 흐릅니다.)