자기장 속에서 고리 전류가 회전할 때 자기력에 의해 작용하는 토크 구하기
안녕하세요, 설군입니다.

자기 쌍극자의 개념을 이용하여 예제 문제를 풀어봅시다.
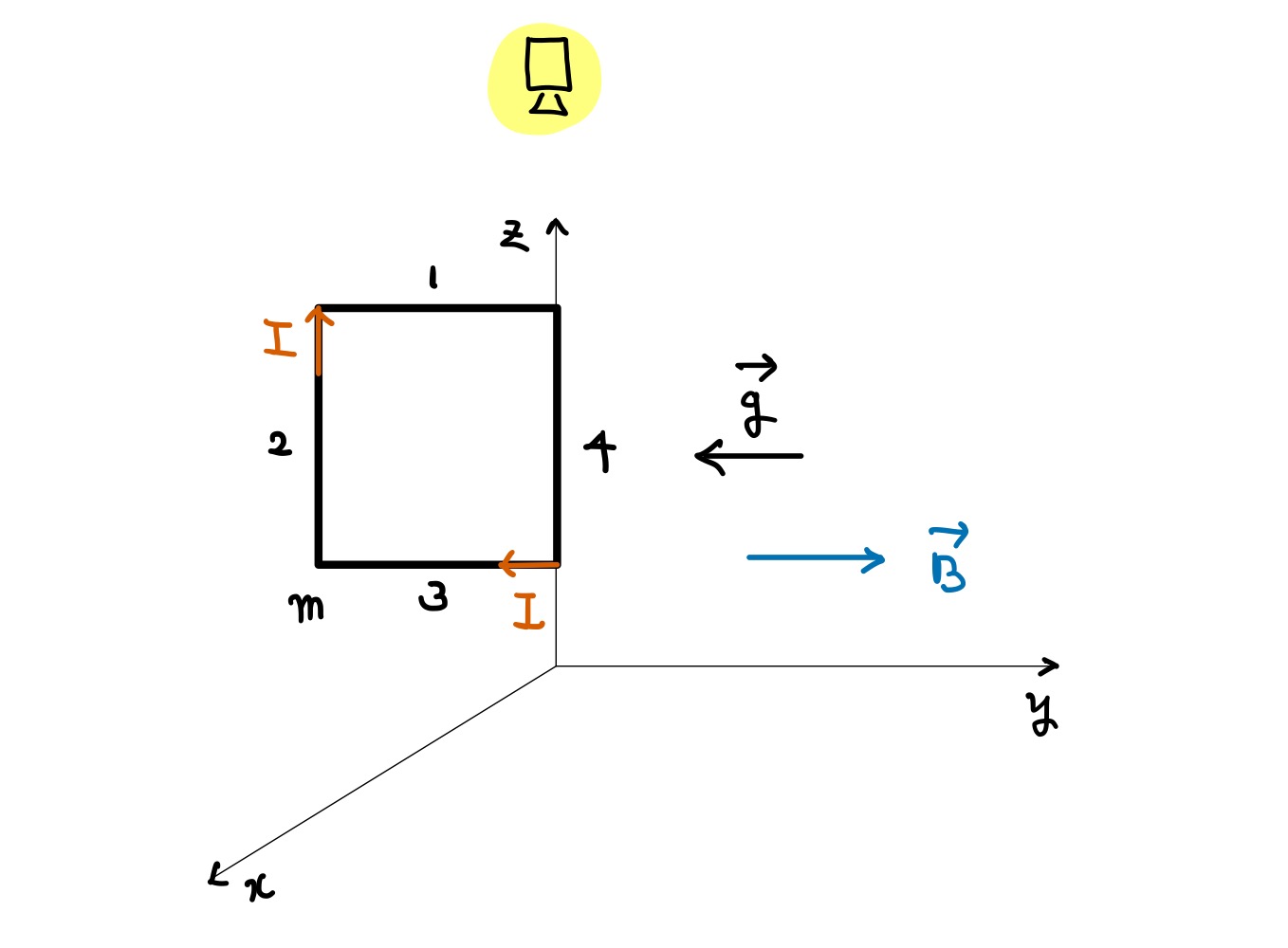
위의 그림과 같이 $x, y, z$ 축을 잡고, 전류가 흐르는 도선을 두었습니다. 도선의 (4) 라고 쓰여진 부분은 $z$ 축에 고정되어 있습니다. 그리고 전류는 그림에서 표시한 것과 같은 방향으로 흐르고 있습니다.
고려해야될 사항은, $+y$ 방향으로 펼쳐진 균일한 자기장과, $-y$ 방향으로 작용하는 중력입니다. 그리고 도선의 질량은 $m$ 입니다.

그림에서 표시한 카메라의 방향에서 계를 내려다 보면 위와 같은 상황이 됩니다. 카메라에서 쳐다보았을 때에는 도선의 2번과 4번 부분이 보일테고, 4번 부분에서는 전류가 들어가는 방향으로 흐르며, 2번 부분에서는 전류가 나오는 방향으로 흐릅니다. 그리고 사각형 도선에 전류가 흐르고 있으므로, 그 사각형 도선의 자기 모멘트를 정의할 수 있습니다.
자기 모멘트의 방향은, 고리에 전류가 흐르는 방향을 오른손 네 손가락으로 감아쥐었을 때 엄지 손가락이 향하는 방향입니다. 엄지 손가락이 향하는 방향이 자기 모멘트 $\vec{\mu}$ 의 방향이므로 그림에서 표시한 방향입니다.

그림상에서, 자기 모멘트 $\vec{\mu}$ 의 방향은 $-x$ 방향이었고, 공간상에 펼쳐진 자기장 $\vec{B}$의 방향은 $+y$ 방향이었습니다. 이런 경우에는, 자기장에 의해서 자기 모멘트가 돌아가게 됩니다. 즉 사각형 도선이 그림과 같이 시계 방향으로 돌아가려고 합니다. 임의의 돌아간 순간에 사각형 도선과 자기장이 이루는 각도를 $\theta$ 라고 합시다. (그리고, 사각형 도선은 가로가 $a$, 세로가 $b$ 입니다. 즉 2, 4 번 부분의 길이가 $a$, 1, 3 번 부분의 길이가 $b$ 입니다.)
자기장이 자기 모멘트에 작용하는 토크는 다음과 같이 구합니다. 토크의 크기와 방향을 따로 생각해서 구해도 됩니다. 먼저 방향에 대해 생각해보면, 자기 모멘트 벡터와 자기장 벡터의 외적이므로 그 외적의 결과의 방향은 위의 그림상에서 화면을 뚫고 들어가는 방향입니다. (즉 $-z$ 방향)
그리고 외적의 크기는 다음과 같이 구할 수 있습니다.

$\vec{\mu} = I \vec{A}$ 의 식을 이용하여 구할 수 있는데, 여기서 자기 모멘트의 크기는 $\mu = IA$ 가 되고, $A$ 는 사각형 도선의 면적을 의미하므로, $ab$ 가 됩니다.
여기까지가 자기장이 자기 모멘트에 작용하는 토크를 구하는 내용입니다.
그런데 물체가 중력도 받고 있으므로, 중력에 의한 토크도 구해봅시다!
간단하게, 위에서 사용한 그림을 다시 들여다보면 쉽게 구할 수 있습니다.

그림에서 헷갈리지 말아야 할 게 있는데, 2번 지점과 4번 지점 사이의 중심이 회전축이 아니라, 4번 지점이 고정되있으므로 회전축이라는 걸 헷갈리면 안됩니다. 따라서 고리의 중심 즉 무게중심에 중력이 작용한다고 생각 하고 토크 식을 계산하면 됩니다.
토크를 계산하기 위한 팔의 길이는 $b/2$ 가 될 것이고, 토크를 만드는 중력의 크기는 $mg$ 가 되므로,

이와 같이 구할 수 있습니다.
들여다 보면, 자기장에 의한 토크의 방향과 중력에 의한 토크의 방향이 반대 방향이므로 특정 조건을 만족하면 알짜 토크가 0이 되는 순간을 구할 수 있습니다. 그 조건은 자기장에 의한 토크의 *크기*와 중력에 의한 토크의 *크기*가 같은 상황이 되겠죠?
