유전체가 포함된 축전기
안녕하세요, 설군입니다.

간단한 평행판 축전기에 대해서 생각할 때에는, 축전기 사이에 아무것도 차 있지 않은, 그냥 공기인 상황을 생각했었습니다. 그런데 축전기의 전기 용량을 늘리기 위해서 축전기의 중앙에 절연체를 삽입하여 만들 수 있습니다. 절연체는 유전체라고도 말합니다.
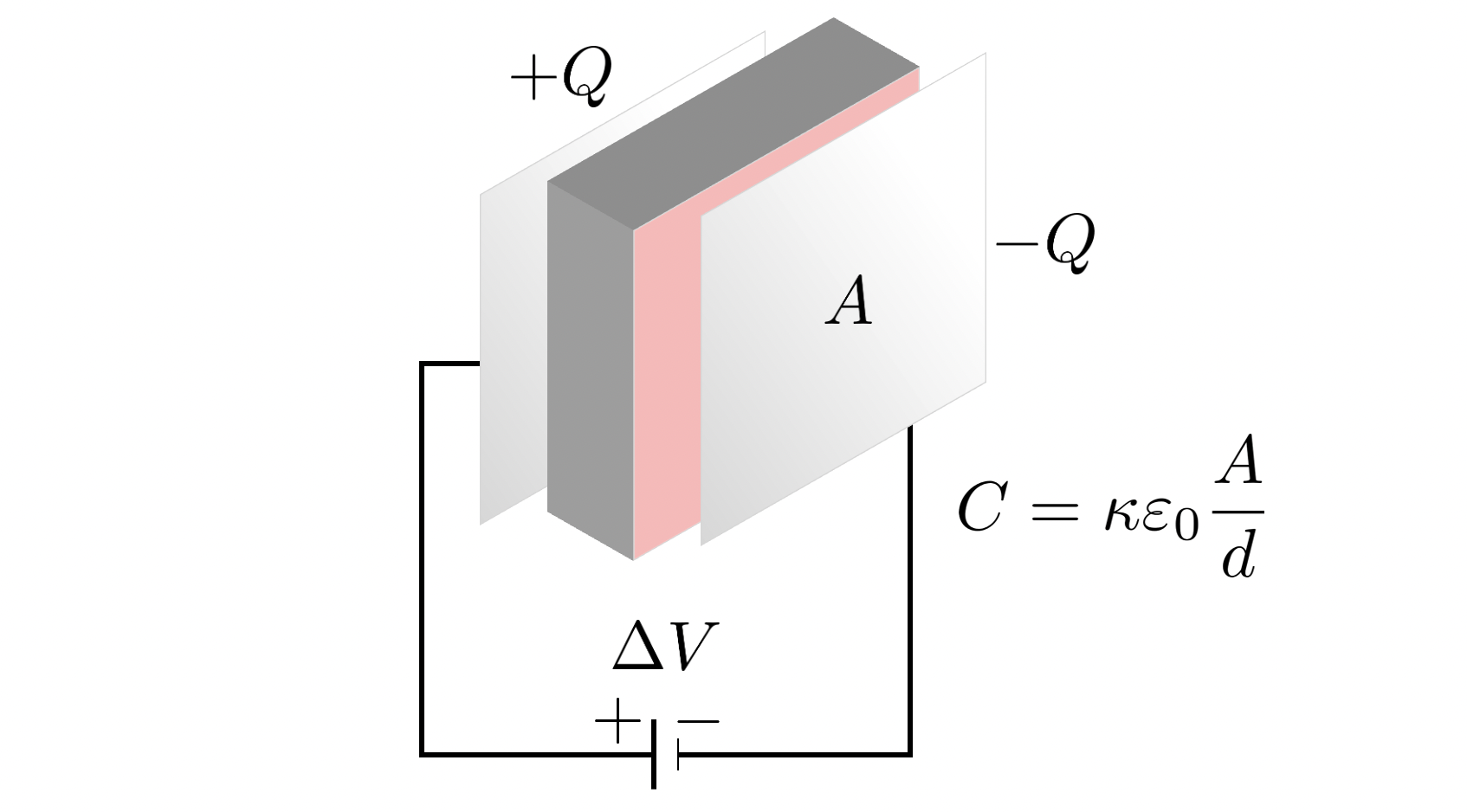
그림과 같이 평행판 축전기 사이에 절연체를 삽입하면, 축전기의 전기 용량은 절연체의 종류에 따라 다른데 증가하게 됩니다.
$$ \varepsilon_0 \frac{A}{d} \rightarrow \kappa \varepsilon_0 \frac{A}{d} $$
이렇게, 축전기의 면적과 극판 사이 간격은 일정한데 유전체가 삽입된 것 만으로 $\kappa$배 증가하게 됩니다. 참고로 $\kappa$는 유전 상수라고 불리는데, 값은 항상 1보다 큰 값입니다.
공기의 유전 상수는 1에 가깝고, 진공인 경우는 정확히 1이며, 종이 같은 경우는 3.7정도 된다고 합니다.
축전기의 전기용량 유전체 없이 크게 만들고 싶을 때에는, 면적을 넓게 하고 간격을 가깝게 해야 합니다. 그런데 간격을 최대한 가깝게 하더라도 실제로는 극판이 닿을 위기에... 놓이기 때문에 그렇게까지 가깝게는 할 수 없어요. 하지만 아주 얇은 종이같은 유전체를 넣게 되면 유전 상수배 만큼 전기 용량이 증가할 뿐더러 두 극판 사이가 닿지 않도록 거리를 매우매우 가깝게 할 수 있기 때문에 많은 이점이 있습니다.
* 예제
다음 그림과 같이 축전기에 유전체가 전부가 아니라 일부만 채워져 있는 경우에 전기 용량이 어떻게 변하는지를 살펴봅시다.

이와 같이 축전기 극판 사이 거리는 $d$만큼 떨어져 있는데, 유전체가 채워진 두께는 $fd$라고 합시다. 이 상황은 다음 상황과 동일합니다.

유전체가 꽉 채워진 축전기와, 아무것도 채워지지 않은 축전기가 직렬로 연결된 상황입니다. 이 상황과 동일하므로, 유전체가 채워진 축전기의 전기 용량을 $C_1$, 채워지지 않은 축전기의 전기 용량을 $C_2$라고 한다면, 축전기의 직렬 연결 식에 의해 총 축전기의 전기 용량은
$$ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} $$
가 됩니다.
먼저 유전체가 채워진 축전기의 전기 용량 식을 써 보면, (단, 축전기 극판의 면적은 $A$라고 합시다)
$$ C_1 = \kappa \varepsilon_0 \frac{A}{fd} $$
가 됩니다.
유전체가 채워지지 않은 축전기의 전기 용량 식은,
$$ C_2 = \varepsilon_0 \frac{A}{d(1-f)} $$
가 됩니다.
따라서 계산식은
$$ \frac{1}{C} = \frac{fd}{\kappa \varepsilon_0 A} + \frac{\kappa (1-f) d}{\kappa \varepsilon_0 A} = \frac{f+ \kappa (1-f) }{\kappa} \frac{d}{\varepsilon_0 A} $$
이므로, 최종적인 전기 용량 $C$는,
$$ C = \frac{\kappa}{f + \kappa (1-f)} \frac{\varepsilon_0 A}{d} $$
이 됩니다.
