| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 베르누이
- 자체유도계수
- 거울의 작도
- 운동량
- 운동 방정식
- 모의고사
- 부력
- 상의 작도
- 등가속도 그래프
- 전기장
- 등가속도 운동
- 상호유도계수
- 움직 도르래
- 전기력
- 물리 2
- 물리학
- 파동
- 렌즈
- 회로
- 벡터의 분해
- 자기장
- 에너지
- 거울
- 도르래
- 렌즈 공식
- 열역학
- 렌즈 제작자 공식
- 운동방정식
- 돌림힘
- 고정 도르래
- Today
- Total
설군의연구소
미분 방정식의 기본적인 개념 본문
안녕하세요, 설군입니다.
물리학에서는 미분 방정식이 매우 많이 등장합니다. 뉴턴의 법칙 중 하나인 *가속도의 법칙* 또한 미분 방정식의 일종이고, 양자역학에서 유명한 *슈뢰딩거 방정식* 또한 미분 방정식의 일종입니다.
대학생 때 물리학과 과목으로 개설되었던 *미분 방정식* 이라는 과목을 재미있게 공부했던 기억이 있습니다.
Dennis G. Zill 의 A first course in differential equations with modeling applications, 10th 교과서로 공부하였습니다.
(한글 제목으로는 *미분방정식 입문* 입니다.)
미분 방정식은 도함수를 포함하는 방정식입니다.
일계 미분이냐, 이계 미분이냐 상관 없이 포함만 되어 있으면 미분 방정식입니다.
만약 $y'$ 을 포함한다면, 미분 방정식을 풀어서 해를 구한다는 말은 $y$ 라는 함수를 구한다는 말입니다.
$$ x^2 + 5x + 4 = 0 $$
이라는 방정식을 해결한다는 말은? $x$ 값을 찾는다는 말입니다.
미분 방정식에서는
$$ y'' + 2y' + y = 0 $$
이런 식으로 생겼는데, 뭐에 대해서 $y$ 라는 함수를 미분했는지는 모르겠지만,
$y''$ 는 $y$ 라는 함수를 두 번 미분했다는 뜻이고, $y'$ 는 한 번 미분했다는 뜻입니다.
어쨌든 계속 강조하지만, $y$ 라는 함수를 구하는 것이 바로 미분 방정식을 푸는 것입니다.
* 상미분 방정식 (Ordinary differential equation, ODE)
미분 방정식은 다양한 꼴이 있습니다.
$$ \frac{dy}{dx} + 4y = e^x $$
$$ \frac{d^2y}{dx^2} - \frac{dy}{dx} + 5y = 0 $$
$$ \frac{dx}{dt} + \frac{dy}{dt} = 2x + 2y $$
등등 다양한 꼴이 있는데, 위의 미분 방정식들은 상미분 방정식이라고 합니다.
1. 독립 변수가 하나 (첫 번째 식의 경우에는 독립 변수가 $x$, 두 번째 식의 경우에는 독립 변수가 $x$, 세 번째 식의 경우에는 독립 변수가 $t$)
2. 종속 변수가 하나 이상
즉, 하나에 대해서만 미분하는 것들은 다 상미분 방정식입니다.
* 편미분 방정식 (Partial differential equation, PDE)
편미분 방정식 이라는 것들도 있습니다.
$$ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0 $$
$$ \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} $$
이런 것들은 미분 하는게 $x$ 에 대해서만 미분하는 게 아니라, 두 변수에 대해서 미분하죠? 이런 것들은 편미분 방정식이라고 합니다.
(슈뢰딩거 방정식은 기본적으로 편미분 방정식 입니다. 물리량을 시간에 대해 미분하기도 하고, 공간에 대해 미분하기도 합니다.)
도함수의 계수가 높아질 때에는
$$ y'''' \rightarrow y^{(4)} $$
이런 식으로 표현하거나,
$$ \frac{d^4 y}{dx^4} $$
이렇게 표현됩니다.
물리학에서는 물체의 운동을 기술하기 위해서, 물체의 위치를 시간에 대해 나타낸 함수, 물체의 속도를 시간에 대해 나타낸 함수, 물체의 가속도를 시간에 대해 나타낸 함수를 주로 다음과 같이 표현합니다.
$$ x(t), v(t), a(t) $$
주로 시간에 대해 함수가 어떻게 변하는지 (물체의 위치가 시간에 대해 어떻게 변하는지) 가 관심사이므로, 보통 시간에 대해 미분합니다.
그래서 시간에 대한 미분은 함수 위에 점을 찍어 표현하곤 합니다.
$$ \dot{x} (t), \dot{v} (t), \ddot{x} (t) $$
이런 식으로요. 한 번 점을 찍으면 시간에 대해 한 번 미분했다는 뜻이고, 두 번 점을 찍으면 두 번 미분했다는 뜻입니다.
* 미분 방정식의 명칭 (n계 m차 미분 방정식)
$$ \frac{d^2 y}{dx^2} + 5 \left( \frac{dy}{dx} \right) ^3 - 4y = e^x $$
이와 같은 미분 방정식은, 2계 1차 미분 방정식이라고 합니다. 최고계 도함수 (식에서 가장 많은 미분이 있는 항) 의 계수가 가장 첫번째 항이므로 2계 라는 이름이 붙고, 1차 라는건 그 최고계 도함수가 몇제곱이냐의 의미입니다. 첫번째 항이 최고계 도함수인데 제곱이 없으므로 그냥 1차 입니다. 그래서 2계 1차 미분 방정식 이라고 합니다.
$$ \left( \frac{d^2 y}{dx^2} \right)^3 = \sqrt{1+\frac{dy}{dx}} $$
이 경우는, 최고계 도함수가 2계 미분이므로 2계고,
그게 세제곱 이므로 3차. 즉 2계 3차 미분 방정식...
이 아닙니다!
제곱근을 풀어줘서 봐줘야 합니다.
$$ \left( \frac{d^2 y}{dx^2} \right)^6 = 1 + \frac{dy}{dx} $$
이렇게 보면, 2계 6차 미분 방정식 입니다.
미분 방정식은 식을 어떻게 정리하느냐에 따라서, 모양은 달라 보이지만 같은 미분 방정식인 경우가 있습니다.
$$ (y-x)dx+4xdy=0 $$
이렇게 쓰여진 식이 있다면,
$$ \frac{dy}{dx} = y' $$
으로 치환해서 정리하면,
$$ (y-x) + 4xy'=0 $$
혹은
$$ 4xy' + y =x $$
이런 식으로 변형될 수도 있습니다.
* 선형 미분 방정식
미분 방정식이 주어졌을 때, 그 미분 방정식이 선형이라고 하려면, 다음 조건을 만족해야 합니다.
1. 종속 변수 $y$ 와 모든 도함수 $y', y'', y''', ...$ 의 차수가 1차이다.
2. $y', y'', y''', ...$ 의 계수는 독립변수 $x$ 에만 의존해야 한다.
예를 들어, 위에 주어진 미분 방정식
$$ 4xy' + y = x $$
의 경우에는, 종속 변수와 도함수 의 차수가 1차이고, $y, y', y''', ...$ 에 붙은 계수가 $x$ 에 대한 식밖에 없으므로
선형 미분 방정식이 맞습니다.
$$ y'' - 2y' + y = 0 $$
이라는 미분 방정식이라면, 이것도 선형 미분 방정식입니다.
$$ (1-y) y'' + 2y = 0 $$
이건 선형 미분 방정식이 아닙니다. 첫 번째 항에서의 계수가 $y$ 에 대한 식이니까요.
$$ y'' + \sin (y) = 0 $$
이 때에는, 두 번째 항에서 $y$ 의 차수가 1차가 아니라서 비선형 미분 방정식입니다.
$$ y^{(4)} + y^2 = 0 $$
이 경우에는, $y$ 의 차수가 2 이므로 비선형입니다.
* 미분 방정식의 해
미분 방정식의 해를 찾았다고 합시다. 즉 $y$ 를 찾은 것이죠. 이 $y$ 를 원래의 미분 방정식에 넣으면 당연히 방정식을 만족해야 합니다.
$$ y'' - 2y' + y =0 $$
이라는 미분 방정식에서,
$$ y = xe^x $$
는 해인지 살펴봅시다. $x$ 에 대해 한 번 미분한 결과도 대입해야 되고, 두 번 미분한 결과도 대입해야 합니다.
$$ y' = e^x + xe^x $$
$$ y'' = e^x + e^x + xe^x $$
이므로, 대입해주면?
$$ y''-2y'+y = 2e^x + xe^x - 2(e^x + xe^x) + xe^x $$
정리해주면 이 결과는 $0$ 이 되므로, 원래의 미분 방정식을 만족하는 것을 알 수 있습니다.
미분 방정식의 해는, 미분 가능합니다. 그러므로 연속이어야 합니다.
* 일반해 (General solution) 와 특수해 (Particular solution)
미분 방정식의 해를 구했을 때에는, 몇 가지 경우로 나뉩니다.
일반해의 경우, 해를 구하고 나서 상수가 $C$ 로 남아있는 상황입니다. 특수해는, 해를 구했는데 상수가 남아있지 않은 상황을 말합니다.
$$ xy' - y = x^2 \sin(x) $$
라는 미분 방정식을 풀어서, $ y = C x - x \cos (x) $ 라는 해가 나왔습니다. 이 해는 상수가 있으므로 일반해 입니다.
미분 방정식의 일반해의 상수를 찾아주기 위해서는 초기조건 이라는 게 필요한데,
미분 방정식이
$$ y \left( \frac{\pi}{2} \right) = 0 $$
이라는 조건을 만족한다고 합시다. 그렇다면 상수 $C$ 를 찾아줄 수가 있어요.
$$ y = -x \cos (x) $$
그렇게 구한 위의 해는 특수해 라고 합니다.
물리학 문제에서는 초기조건을 주는 경우가 많습니다. 가령 물체의 위치가 시간이 0일 때에는, 원점에 있었다거나. 물체의 속도가 시간이 0일 때에는 0 이라거나...
미분 방정식에서 도함수의 계수와 상수의 개수가 일치한다는 사실을 알아두면 좋습니다.
2계 미분 방정식이면, 일반해에서 임의의 상수가 두 개가 나옵니다.
그리고 그 상수 두 개를 찾기 위해서는 초기조건도 두 개가 필요합니다.
* 특이해 (Singular solution)
$$ \frac{dy}{dx} = x y^{\frac{1}{2}} $$
이런 미분 방정식이 있고, 일반해가
$$y = \left( \frac{1}{2} x^2 + C \right) ^2 $$
초기조건이 $y(x=0) = 0 $ 일 때의 특수해가
$$ y = \frac{1}{16} x^4 $$
이라고 합니다.
그런데 신기하게도, 그냥 $y=0$ 을 대입해도 미분 방정식을 만족합니다. 이런 $y=0$ 과 같은 해를 *특이해* 라고 합니다.
일반해의 상수에 어떤 값을 넣더라도 이 해는 나올수가 없습니다.
이런 특이해는 비선형 미분 방정식에서 자주 나타납니다.
* 특수해와 임의의 상수
$$ x'' + 16 x = 0 $$
어떤 미분 방정식을 풀었는데, 만족하는 두 개의 해가 나왔다고 합니다.
$$ x_1 = C_1 \cos (4t) $$
$$ x_2 = C_2 \sin (4t) $$
이 경우는 2계 미분 방정식이므로, 임의의 상수가 두 개 나와야 하는데, 해가 두 개이고 상수가 각각 하나씩 나오긴 했네요.
그런데 신기하게도 이 두 해 $x_1, x_2$ 를 선형 결합 (그냥 더한다) 해주면?
$$ x = C_1 \cos(4t) + C_2 \sin (4t) $$
로 적을 수 있는데, 이것도 해입니다. 이 경우도 임의의 상수가 두 개인 해를 찾았다고 볼 수 있죠.
* 초기조건의 조건
$$ \frac{d^n y}{dx^n} = f(x, y, y', y'', ..., y^{(n-1)}) $$
의 특수해를 구하기 위해서는 초기조건이 $n$ 개 필요합니다.
그런데, 그 초기조건의 조건이 있습니다. 대입하는 $x$ 값이 다음과 같이 동일해야 합니다.
$$ y(x_0) = y_0 $$
$$ y'(x_0) = y_1 $$
$$ y''(x_0) = y_2 $$
...
이런 식으로 동일해야 합니다.
* 초기값 문제 (Initial value problem)와 함수의 그래프, 해의 그래프
초기조건이 주어진 미분 방정식의 해를 구하는 것을 초기값 문제라고 합니다. (초깃값?)
1계 초기값 문제, 2계 초기값 문제... 이런식으로 부릅니다.
$$ y' + 2xy^2 = 0 $$
이라는 미분 방정식의 일반해가
$$ y = \frac{1}{x^2 + C} $$
이고, 초기조건이 $ y(x=0) = -1 $ 일 때 특수해가
$$ y = \frac{1}{x^2-1} $$
이라고 합니다. 이 특수해의 그래프를 그려보면
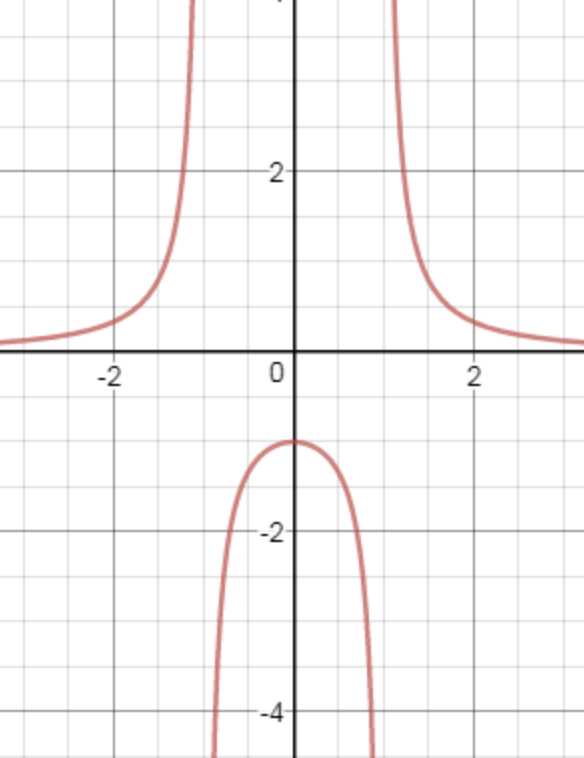
이렇게 그려지는데, 초기조건을 만족하는 부분을 들여다봅시다. $x=0$ 일 때는 $y=-1$ 입니다. 내가 그린 그래프가 초기조건을 잘 만족하네요. 그런데
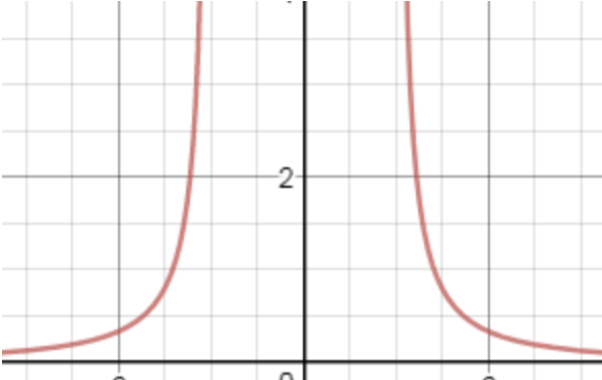
요 부분은 함수의 그래프이긴 하지만, 초기조건과이 만족되지 않는 부분의 그래프이므로, 단지 함수의 그래프일 뿐, 해의 그래프가 아닙니다.
해의 그래프는
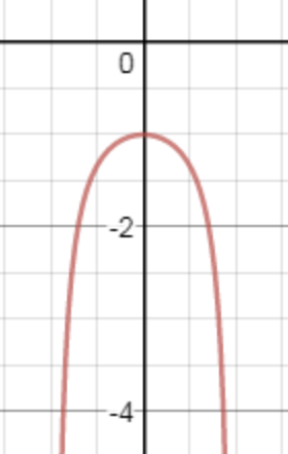
이 부분입니다.
* 초기조건의 낚시
$$ y'' + 4y = 0 $$
$$ y = C_1 \cos(2x) + C_2 \sin (2x) $$
위와 같이 미분 방정식이 주어졌고, 일반해가 주어진 상황입니다. 초기조건이
$$ y'\left( \frac{\pi}{2} \right) = 1, y'(\pi) = 0 $$
이라고 주어졌다고 합시다. 이 초기조건을 대입해서 상수를 찾아보면,
$$ C_1 = 0, C_2 = 2 $$
이렇게 나옵니다... 어라... 상수 하나가 필요가 없네요. 마치 모순인 것 같습니다.
하지만 낚이면 안 됩니다. 초기조건을 대입하기 위해서는 동일한 $x$ 값일 때의 초기조건이 주어져야 합니다.
그러므로 주어진 것 만으로는 이 미분 방정식의 해를 구할 수가 없습니다.

