| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 돌림힘
- 전기력
- 물리 2
- 운동량
- 렌즈 공식
- 자체유도계수
- 회로
- 자기장
- 상의 작도
- 베르누이
- 등가속도 그래프
- 파동
- 움직 도르래
- 렌즈
- 거울
- 전기장
- 에너지
- 물리학
- 벡터의 분해
- 고정 도르래
- 열역학
- 부력
- 운동 방정식
- 거울의 작도
- 렌즈 제작자 공식
- 모의고사
- 등가속도 운동
- 상호유도계수
- 도르래
- 운동방정식
- Today
- Total
설군의연구소
임의의 곡선 모양 빗면에서의 물체의 운동 방정식 본문
안녕하세요, 설군입니다.
다음과 같이 평평하고, 지면으로부터의 각도가 $\theta$ 인 빗면에서 물체가 받는 힘을 모조리 분석해봅시다.

물체가 받는 중력은 아래 방향으로 $mg$ 입니다. 그리고 빗면과 수직한 방향으로 수직항력 $N$ 을 받습니다. 이 수직항력을 $x$, $y$ 방향으로 각각 분해하기 위해 빗면 각도 $\theta$ 를 요리조리 잘 분석하여 각도를 표시해봅니다.
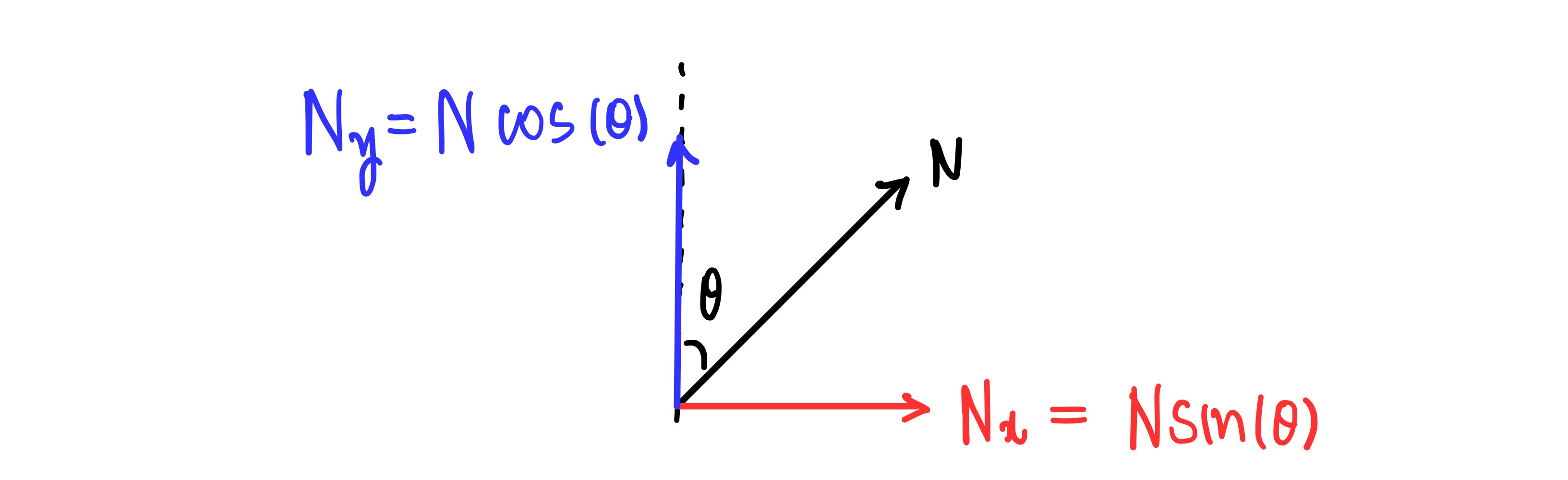
잘 표시해보면 이렇게 닮은꼴 삼각형을 찾을 수 있습니다. 물체가 받는 수직항력의 $x$ 성분은 $N_x$ 로 표시하였고, sine 이 곱해진 값이 됩니다. 물체가 받는 수직항력의 $y$ 성분은 $N_y$ 로 표시하여, cosine 이 곱해진 값이 됩니다.

따라서, 빗면의 각도가 $\theta$ 인 평평한 빗면에 물체가 놓여있을 때, 물체가 받는 중력과 수직항력을 분해해보면 위와 같이 됩니다.
그리고 나서는 $x$, $y$ 방향에 대해 각각 운동 방정식을 세워야 합니다.
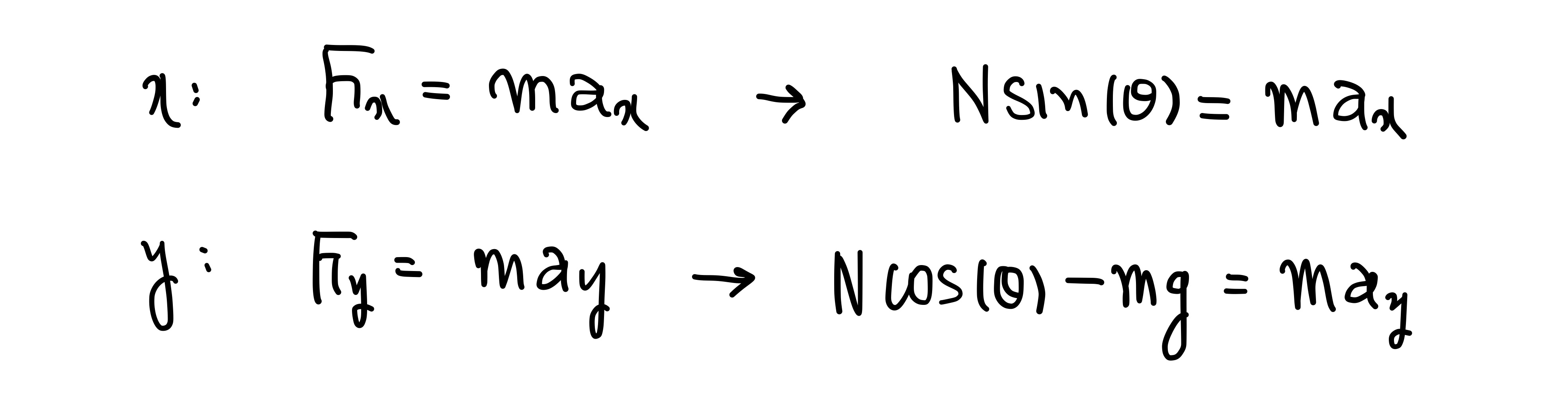
간단하게 위와 같이 됩니다. 이 때, 오른쪽 방향을 $+x$ 좌표로, 위쪽 방향을 $+y$ 좌표로 잡았습니다.
만약 물체가 평평한 빗면이 아니라, 임의의 곡선에 놓여있다면 어떻게 될까요? 예를 들어 $y=x^2$ 모양의 빗면에 놓여 있다고 생각합니다.
물체가 높은 곳에서 미끄러지며 오른쪽으로 이동하는 상황을 가정하기 위해, $y=x^2$ 곡선의 $x<0$ 부분만 생각해봅시다.

임의의 $x$ 좌표, $-x$ 인 파란색으로 표시한 지점에서 순간 접선을 구하면, 그 접선을 평평한 빗면이라고 생각할 수 있습니다.
그 평평한 빗면의 각도를 $\theta$ 라고 생각하고 그 각도를 구하기 위해서는, 그 접선의 기울기 자체를 구하면 됩니다.
그 접선의 기울기는 다름이아닌 $dy/dx$ 이므로, 그 기울기는 $2x$ 인 셈입입니다. 그런데 여기서 각도를 구하기 위해서는 탄젠트의 역함수를 이용하면 됩니다.
각도를 양수로 나타내기 위해서는, 탄젠트의 역함수의 절댓값을 구한다고 생각하면 됩니다. 정리하자면 결국 임의의 $-x$ 지점에서의 빗면의 기울기는 $\theta = \arctan (2x)$ 입니다.
평평한 빗면일 때에는 물체의 수직항력 성분이 $\theta$ 가 일정하니까, 변하지 않았는데 이와 같이 $y=x^2$ 같은 곡선에서는 매 $x$ 값마다 접선이 바뀌게 되므로, 각도 $\theta$ 가 변하게 됩니다. 즉 매 순간 수직항력이 변하게 됩니다.

힘을 구했으니, 운동 방정식을 세워봅시다. ($F=ma$) $\ddot{x}$ 와 같은 형태로 표현한 건, 시간에 대해 두 번 미분했다는 의미입니다. 시간에 대해 한 번 미분한 경우에는 $\dot{x}$, 두 번 미분한 경우에는 $\ddot{x}$ 의 형태로 표현합니다.

각각의 축으로 운동 방정식이 세워지므로 두 개의 방정식이 나옵니다. 그런데 식에서 cosine과 sine이 보입니다. 이를 tangent로 나타내기 위해서 서로 나누어보면 위와 같이 정리할 수 있습니다.

앞서 말한대로, tangent가 바로 접선의 기울기이기 때문에, $-x$ 지점에서 접선의 기울기는 $dy/dx$ 에 $x$ 대신 $-x$ 를 대입해준 값, 즉 $-2x$ 입니다. 그래서 위와 같이 $\ddot{x}$ 와 $\ddot{y}$ 에 관한 관계식으로 정리되었습니다.
마지막으로 위의 미분 방정식을 정리하는 방법은 간단합니다. 모조리 $x$ 에 관한 식으로 만들어주기 위해서, $y=x^2$ 이라는 곡선의 방정식으로부터 무언가를 이끌어낼 것입니다.
$y=x^2$ 이라는 곡선의 방정식을, 차근차근 시간에 대해 미분 한번, 두번 하여 식을 얻어내는 과정입니다.
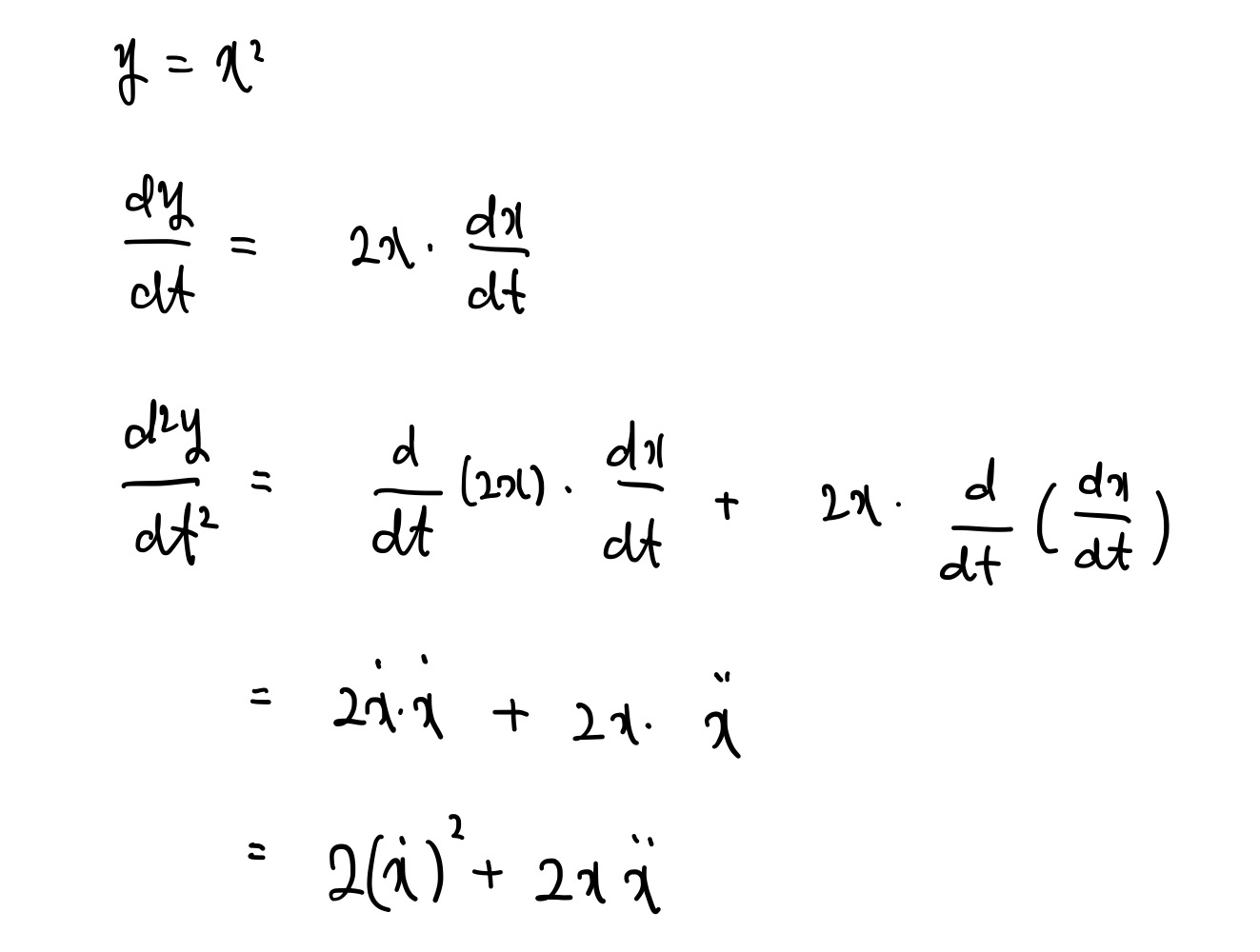
이렇게 곡선의 방정식을 시간에 대해 두 번 미분하여, $\ddot{y}$ 를 $\ddot{x}$ 와 $\dot{x}$ 로 표현할 수 있게 되었습니다. 그렇다면 이 식을 대입해주면 정리가 끝납니다.

최종적으로는
$$ \ddot{x} = -2x (2 \dot{x}^2 + 2x \ddot{x} +g) $$
의 꼴로 정리가 되는데, 이 미분 방정식을 풀기만 하면 $x(t)$ 를 구할 수 있습니다.
그런데 이는 해석적으로 $x(t) = ... $ 의 꼴을 구하기는 어려운 것 같고요, 수치적으로 구해서 그래프를 그려볼 수는 있습니다.
아무튼, 물체의 운동 궤적을 구하기 위해 가장 먼저 접근해봐야 할 방법은 운동 방정식을 세워 미분 방정식을 푸는 것입니다.
미분 방정식을 푼다는 말은, 내가 구한 미분 방정식에 대입했을 때 그 수식을 만족하는 $x(t)$ 를 구한다는 말입니다. 간단한 미분 방정식의 예시로,
$$\ddot{x(t)} = a^2 x(t)$$
라는 미분 방정식이 있을 때, $x(t) = e^{at}$ 라는 함수는 $\dot{x(t)} = a e^{at}$, $\ddot{x(t)} = a^2 e^{at} $ 이므로, 미분 방정식에 대입해보면,
$$ a^2 e^{at} = a^2 e^{at} $$ 를 만족하므로 해가 됩니다.
'물리학 > 일반물리학' 카테고리의 다른 글
| 고리 도선이 자기장 영역을 통과할 때 (0) | 2024.02.03 |
|---|---|
| ㄷ자 도선에 걸친 금속 막대가 움직일 때 (1) | 2023.12.23 |
| 솔레노이드가 만드는 자기장 예제 (0) | 2023.12.16 |
| 물질이 나타내는 자성 (1) | 2023.11.18 |
| 직선 도선 주변에서의 자기 플럭스 구하기 (1) | 2023.10.14 |





